题目内容
17、如图,把一张长方形的纸片按如图所示的方式折叠,EM、FM为折痕,折叠后的C点落在B'M或B'M的延长线上,那么∠EMF的度数是
90
度.
分析:由折叠可知,∠BME=∠B′ME,∠CMF=∠C′MF,而这四个角的和为180°,从而可求∠EMB′+∠FMC的度数.
解答:解:根据折叠的性质可知,∠BME=∠B′ME,∠CMF=∠C′MF,
∵∠BME+∠B′ME+∠CMF+∠C′MF=180°,
∴2(∠EMB′+∠FMC)=180°,即∠EMB′+∠FMC=90°
∴∠EMF=90°.
∵∠BME+∠B′ME+∠CMF+∠C′MF=180°,
∴2(∠EMB′+∠FMC)=180°,即∠EMB′+∠FMC=90°
∴∠EMF=90°.
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
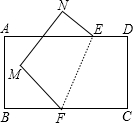 如图,把一张长方形的纸片沿着EF折叠,点C、D分别落在M、N的位置,且∠MFB=
如图,把一张长方形的纸片沿着EF折叠,点C、D分别落在M、N的位置,且∠MFB=| 1 |
| 2 |
| A、30° | B、36° |
| C、45° | D、72° |

 如图,把一张长方形的纸片ABCD沿BD对折,使C点落在E点处,BE与AD相交于点O,图中除了△ABD≌△CDB外,请写出其他一组全等三角形
如图,把一张长方形的纸片ABCD沿BD对折,使C点落在E点处,BE与AD相交于点O,图中除了△ABD≌△CDB外,请写出其他一组全等三角形