题目内容
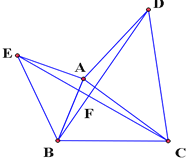
【题目】如图,已知△ABC,分别以AB,AC为直角边,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,连结BD,CE交于点F,设AB=m,BC=n.
(1)求证:∠BDA=∠ECA.
(2)若m=![]() ,n=3,∠ABC=75°,求BD的长.
,n=3,∠ABC=75°,求BD的长.
(3)当∠ABC=____时,BD最大,最大值为____(用含m,n的代数式表示)
(4)试探究线段BF,AE,EF三者之间的数量关系。
【答案】135° ![]() m+n
m+n
【解析】
试题
(1)由已知条件证△ABD≌△AEC,即可得到∠BDA=∠CEA;
(2)过点E作EG⊥CB交CB的延长线于点G,由已知条件易得∠EBG=60°,BE=2,这样在Rt△BEG中可得EG=![]() ,BG=1,结合BC=n=3,可得GC=4,由长可得EC=
,BG=1,结合BC=n=3,可得GC=4,由长可得EC=![]() ,结合△ABD≌△AEC可得BD=EC=
,结合△ABD≌△AEC可得BD=EC=![]() ;
;
(3)由(2)可知,BE=![]() ,BC=n,因此当E、B、C三点共线时,EC最大=BE+BC=
,BC=n,因此当E、B、C三点共线时,EC最大=BE+BC=![]() ,此时BD最大=EC最大=
,此时BD最大=EC最大=![]() ;
;
(4)由△ABD≌△AEC可得∠AEC=∠ABD,结合△ABE是等腰直角三角形可得△EFB是直角三角形及BE2=2AE2,从而可得EF2=BE2-BF2=2AE2-BF2.
试题解析:
(1)∵△ABE和△ACD都是等腰直角三角形,且∠EAB=∠DAC=90°,
∴AE=AB,AC=AD,∠EAB+∠BAC=∠BAC+∠DAC,即∠EAC=∠BAD,
∴△EAC≌△BAD,
∴∠BDA=∠ECA;
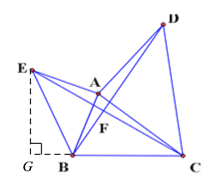
(2)如下图,过点E作EG⊥CB交CB的延长线于点G,
∴∠EGB=90°,
∵在等腰直角△ABE,∠BAE=90°,AB=m=![]() ,
,
∴∠ABE=45°,BE=2,
∵∠ABC=75°,
∴∠EBG=180°-75°-45°=60°,
∴BG=1,EG=![]() ,
,
∴GC=BG+BC=4,
∴CE=![]() ,
,
∵△EAC≌△BAD,
∴BD=EC=![]() ;
;
(3)由(2)可知,BE=![]() ,BC=n,因此当E、B、C三点共线时,EC最大=BE+BC=
,BC=n,因此当E、B、C三点共线时,EC最大=BE+BC=![]() ,
,
∵BD=EC,
∴BD最大=EC最大=![]() ,此时∠ABC=180°-∠ABE=180°-45°=135°,
,此时∠ABC=180°-∠ABE=180°-45°=135°,
即当∠ABC=135°时,BD最大=![]() ;
;
(4)∵△ABD≌△AEC,
∴∠AEC=∠ABD,
∵在等腰直角△ABE中,∠AEC+∠CEB+∠ABE=90°,
∴∠ABD+∠ABE+∠CEB=90°,
∴∠BFE=180°-90°=90°,
∴EF2+BF2=BE2,
又∵在等腰Rt△ABE中,BE2=2AE2,
∴2AE2=EF2+BF2.

【题目】为节约用水,某市居民生活用水按阶梯式水价计量,水价分为三个阶梯,价格表如下表所示:
某市自来水销售价格表
类别 | 月用水量 (立方米) | 供水价格 (元/立方米) | 污水处理费 (元/立方米) | |
居民生活用水 | 阶梯一 | 0~18(含18) | 1.90 | 1.00 |
阶梯二 | 18~25(含25) | 2.85 | ||
阶梯三 | 25以上 | 5.70 | ||
(注:居民生活用水水价=供水价格+污水处理费)
(1)当居民月用水量在18立方米及以下时,水价是_____元/立方米.
(2)4月份小明家用水量为20立方米,应付水费为:
18×(1.90+1.00)+2×(2.85+1.00)=59.90(元)
预计6月份小明家的用水量将达到30立方米,请计算小明家6月份的水费.
(3)为了节省开支,小明家决定每月用水的费用不超过家庭收入的1%,已知小明家的平均月收入为7530元,请你为小明家每月用水量提出建议







