题目内容
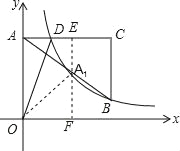
【题目】如图,在平面直角坐标系中,点A坐标(0,6),AC⊥y轴,且AC=AO,点B,C横坐标相同,点D在AC上,tan∠AOD=![]() ,若反比例函数y=
,若反比例函数y=![]() (x>0)的图象经过点B、D.
(x>0)的图象经过点B、D.
(1)求:k及点B坐标;
(2)将△AOD沿着OD折叠,设顶点A的对称点A1的坐标是A1(m,n),求:代数式m+3n的值以及点A1的坐标.

【答案】(1)(6,2);(2)(3.6,4.8)
【解析】
试题(1)先根据tan∠AOD=![]() ,A坐标(0,6)得出AD的长,再根据点D在反比例函数y=
,A坐标(0,6)得出AD的长,再根据点D在反比例函数y=![]() (x>0)的图象上可求出k的值,由BC∥AO,得出B点坐标;
(x>0)的图象上可求出k的值,由BC∥AO,得出B点坐标;
(2)过点A1作EF∥OA交AC于E,交x轴于F,连接OA1,根据AC∥x轴可知∠A1ED=∠A1FO=90°,由相似三角形的判定定理得出△DEA1∽△A1FO,设A1(m,n),可得出![]() ,m2+n2=2m+6n,,再根据勾股定理可得出m2+n2=36,于是得到结论.
,m2+n2=2m+6n,,再根据勾股定理可得出m2+n2=36,于是得到结论.
解:(1)∵点A坐标(0,6),tan∠AOD=![]() ,
,
∴AD=2,
∴D(2,6)
∵点D在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴6=![]() ,解得k=12,
,解得k=12,
∵AC=AO,点B,C横坐标相同,
∴点B、C的横坐标都是6,
∴BC∥AO,
∴B(6,2);
(2)过点A1作EF∥OA交AC于E,交x轴于F,连接OA1,
∵AC∥x轴,
∴∠A1ED=∠A1FO=90°,
∵∠OA1D=90°,
∴∠A1DE=∠OA1F,
∴△DEA1∽△A1FO,
∵A1(m,n),
∴![]() =
=![]() ,
,
∴m2+n2=2m+6n,
∵m2+n2=OA12=OA2=36,
∴m+3n=18,
即m=18﹣3n,
∴(18﹣3n)2+n2=36,
解得n1=6(舍去),n2=4.8,
∴m=18﹣3×4.8=3.6,
即点A1的坐标为(3.6,4.8).

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目