题目内容
（2013•桂林模拟）如图，点A在双曲线y=| 2 |
| x |
| 6 |
| x |
4
4
．分析：长DA交y轴于M，设A的坐标是（a，b），C的坐标是（x，y），求出ab=2，xy=6，则矩形ABCD的面积为6-2，求出即可．
解答：解：
延长DA交y轴于M，
设A的坐标是（a，b），C的坐标是（x，y），
∵点A在双曲线y=
上，点D在双曲线y=
上，且AD∥x轴，
∴ab=2，xy=6，
∴矩形ABCD的面积为6-2=4，
故答案为：4．
延长DA交y轴于M，
设A的坐标是（a，b），C的坐标是（x，y），
∵点A在双曲线y=
| 2 |
| x |
| 6 |
| x |
∴ab=2，xy=6，
∴矩形ABCD的面积为6-2=4，
故答案为：4．
点评：本题考查了反比例函数的有关内容的应用，关键是能根据题意得出ab=2，xy=6．
练习册系列答案
相关题目
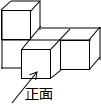（2013•桂林模拟）如图所示的几何体的主视图是（ ）