题目内容
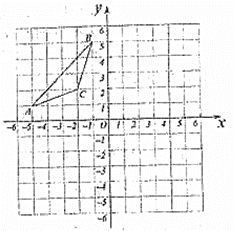
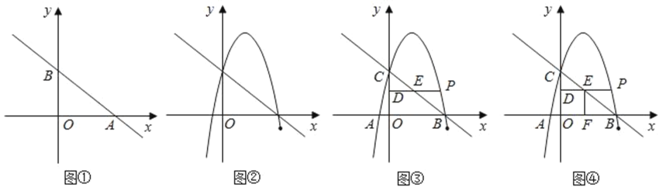
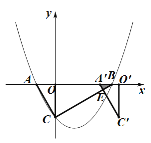
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
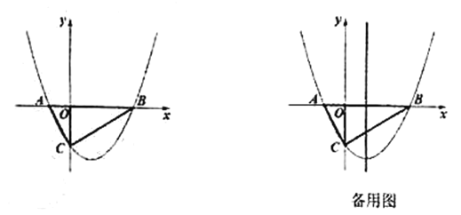
(1)求这个抛物线的解析式;
(2)将![]() 以每秒一个单位的速度沿
以每秒一个单位的速度沿![]() 轴向右平移,平移时间为
轴向右平移,平移时间为![]() 秒,平移后的
秒,平移后的![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 与
与![]() 重合时停止平移,求
重合时停止平移,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)点![]() 在
在![]() 轴上,连接
轴上,连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,若点
,若点![]() 落在这个抛物线的对称轴上,请直接写出所有符合条件的点
落在这个抛物线的对称轴上,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;(3)
;(3)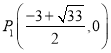 ,
,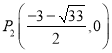
【解析】
(1)抛物线![]() 经过点
经过点![]() ,
,![]() ,把
,把![]() 、
、![]() 坐标代入抛物线解析式求出即可;(2)设
坐标代入抛物线解析式求出即可;(2)设![]() 平移过程中边
平移过程中边![]() 与线段
与线段![]() 的交点为
的交点为![]() ,与线段
,与线段![]() 的交点为
的交点为![]() ,边
,边![]() 与线段
与线段![]() 的交点为
的交点为![]() ,然后表示出
,然后表示出![]() ,本别讨论t的范围,求出S与t的关系即可(3)由于P在x轴上,则可设P(t,0),然后写出CP斜率得到B
,本别讨论t的范围,求出S与t的关系即可(3)由于P在x轴上,则可设P(t,0),然后写出CP斜率得到B![]() 的斜率,然后表示出
的斜率,然后表示出![]() 的坐标,代入二次函数解析式求出t即可
的坐标,代入二次函数解析式求出t即可
解:(1)∵抛物线![]() 经过点
经过点![]() ,
,![]() ,
,
把![]() 、
、![]() 坐标代入抛物线解析式可得:
坐标代入抛物线解析式可得: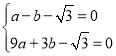 ,
,
解得: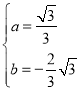 ,
,
∴抛物线解析式为![]() ;
;
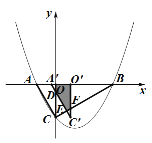
(2)∵![]() ,
,
∴![]() ,
,
设![]() 平移过程中边
平移过程中边![]() 与线段
与线段![]() 的交点为
的交点为![]() ,与线段
,与线段![]() 的交点为
的交点为![]() ,边
,边![]() 与线段
与线段![]() 的交点为
的交点为![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
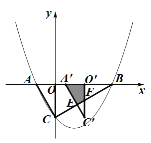
(3) ∵P在x轴上,设P(t,0),则kCP=![]() ,
,
∵B![]() 关于CP对称,则kBB’=
关于CP对称,则kBB’=![]() ,
,
可得CP直线解析式为![]() ;
;
设B![]() 直线解析式为
直线解析式为![]() ,把B(3,0)代入得出b=
,把B(3,0)代入得出b=![]() ,
,
则B![]() 直线解析式为
直线解析式为![]() ,
,
联立两直线解析式![]() ;解得x=
;解得x=![]() ,代入求出y=
,代入求出y=![]() ;
;
求出交点坐标为(![]() );
);
通过中点坐标公式可得![]() 的坐标为(
的坐标为(![]() ,
,![]() ),
),
![]() 在抛物线上,则把
在抛物线上,则把![]() 代入二次函数
代入二次函数![]() ,
,
则![]() ;
;
化简整理得![]()
![]()
![]()
![]()
![]()
故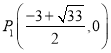 ,
,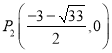

【题目】列方程组解应用题.
某校七年级学生在三月份参加了“学雷锋,献爱心”活动.活动中,1班,2班和3班的同学为希望小学的学生购买了学习用品:书包和词典.已知1班、2班购买的情况如下表:
书包(个) | 词典(本) | 累计花费(元) | |
七年级1班 | 3 | 2 | 124 |
七年级2班 | 2 | 3 | 116 |
活动中,3班购买了4个书包和6本词典,问:3班共花费了多少元?
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
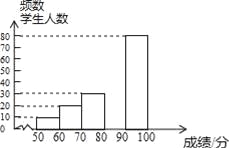
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在_____________分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?