题目内容
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.若A点的坐标为(0,4),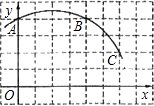 D点的坐标为(7,0),
D点的坐标为(7,0),
(1)圆弧所在圆的圆心M点的坐标为________
(2)点D是否在经过点A、B、C三点的抛物线上;
(3)在(2)的条件下,求证:直线CD是⊙M的切线.
(1)解:连接AB、BC,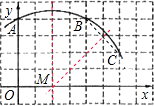
作AB和BC的垂直平分线,两线交于一点,
由图形可知:这点的坐标是(2,0),
∴圆弧所在圆的圆心M点的坐标是(2,0),
故答案为:(2,0).
(2)解:由A(0,4),可得小正方形的边长为1,从而B(4,4)、C(6,2),
设经过点A、B、C的抛物线的解析式为y=ax2+bx+4,
依题意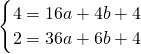 ,解得
,解得 ,
,
所以经过点A、B、C的抛物线的解析式为 ,
,
∵把点D(7,0)的横坐标x=7代入上述解析式,得 ,
,
∴点D不在经过A、B、C的抛物线上.
(3)证明:设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD.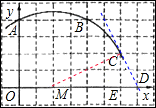
则CE=2,ME=4,ED=1,MD=5,
∵在Rt△CEM中,∠CEM=90°,由勾股定理得:MC2=ME2+CE2=42+22=20,
在Rt△CED中,∠CED=90°,由勾股定理得:CD2=ED2+CE2=12+22=5,
∴MD2=MC2+CD2,
∴∠MCD=90°,
∵MC为半径,
∴直线CD是⊙M的切线.
分析:(1)连接连接AB、BC,作AB和BC的垂直平分线,两线交于一点,则此点就是圆心M,根据图形即可得出答案;
(2)根据图形求出B、C的坐标,设经过点A、B、C的抛物线的解析式为y=ax2+bx+4,代入B、C的坐标求出解析式,把D的坐标代入看看两边是否相等即可;
(3)设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD,得出CE=2,ME=4,ED=1,MD=5,根据勾股定理求出MC2=20,CD2=5,推出∠MCD=90°,根据切线的判定推出即可.
点评:本题考查了勾股定理,切线的判定,用待定系数法求二次函数的解析式等知识点的应用,通过做此题培养了学生的推理能力和计算能力,题目比较典型,但是一道综合性比较强的题目.

作AB和BC的垂直平分线,两线交于一点,
由图形可知:这点的坐标是(2,0),
∴圆弧所在圆的圆心M点的坐标是(2,0),
故答案为:(2,0).
(2)解:由A(0,4),可得小正方形的边长为1,从而B(4,4)、C(6,2),
设经过点A、B、C的抛物线的解析式为y=ax2+bx+4,
依题意
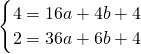 ,解得
,解得 ,
,所以经过点A、B、C的抛物线的解析式为
 ,
,∵把点D(7,0)的横坐标x=7代入上述解析式,得
 ,
,∴点D不在经过A、B、C的抛物线上.
(3)证明:设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD.

则CE=2,ME=4,ED=1,MD=5,
∵在Rt△CEM中,∠CEM=90°,由勾股定理得:MC2=ME2+CE2=42+22=20,
在Rt△CED中,∠CED=90°,由勾股定理得:CD2=ED2+CE2=12+22=5,
∴MD2=MC2+CD2,
∴∠MCD=90°,
∵MC为半径,
∴直线CD是⊙M的切线.
分析:(1)连接连接AB、BC,作AB和BC的垂直平分线,两线交于一点,则此点就是圆心M,根据图形即可得出答案;
(2)根据图形求出B、C的坐标,设经过点A、B、C的抛物线的解析式为y=ax2+bx+4,代入B、C的坐标求出解析式,把D的坐标代入看看两边是否相等即可;
(3)设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD,得出CE=2,ME=4,ED=1,MD=5,根据勾股定理求出MC2=20,CD2=5,推出∠MCD=90°,根据切线的判定推出即可.
点评:本题考查了勾股定理,切线的判定,用待定系数法求二次函数的解析式等知识点的应用,通过做此题培养了学生的推理能力和计算能力,题目比较典型,但是一道综合性比较强的题目.

练习册系列答案
相关题目
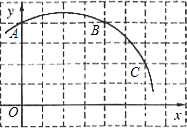 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.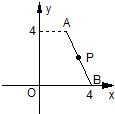 12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )
12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )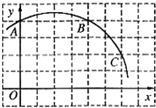 7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )
7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )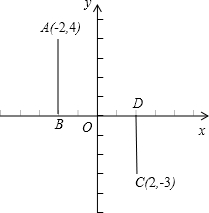 如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标:
如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标: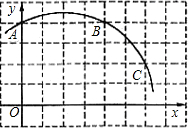 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).