题目内容
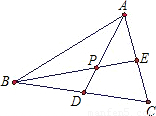
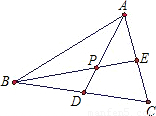
 如图,AD、BE为△ABC的高,AD、BE相交于点F,已知∠ACB=60°,∠ABC=45°.猜测DF与AC间有何数量关系?请说明理由.
如图,AD、BE为△ABC的高,AD、BE相交于点F,已知∠ACB=60°,∠ABC=45°.猜测DF与AC间有何数量关系?请说明理由.分析:根据AD⊥BC,∠ABC=45°,易求∠BAD=45°,从而可得AD=BD,再根据∠ADC=90°,∠ACB=60°,易求∠DAC=30°,而∠AEB=90°,易求∠AFE=60°,那么∠BFD=60°,也就是∠DBF=30°,从而可求∠ACD=∠BFD,利用AAS可证△BDF≌△ACD,从而有BF=AC,在Rt△BDF中,易知∠DBF=30°,根据30°的角所对的便等于斜边的一半,可得DF=
BF,
进而有DF=
AC.
| 1 |
| 2 |
进而有DF=
| 1 |
| 2 |
解答:解:DF=
AC.
∵AD⊥BC,
∴∠ADB=90°,
∵∠ABC=45°,
∴∠BAD=45°,
∴∠ABD=∠BAD,
∴AD=BD,
∵∠ADC=90°,∠ACB=60°,
∴∠DAC=30°,
∵BE⊥AC,
∴∠AEB=90°,
∴∠AFE=90°-30°=60°,
∴∠BFD=∠AFE=60°,
∴∠ACD=∠BFD,
在△BFD和△ACD中,∠ACD=∠BFD,∠ADC=∠BDF=90°,BD=AD,
∴△BDF≌△ACD,
∴BF=AC,
在Rt△BDF中,∠BFD=60°,那么∠DBF=30°,
∴DF=
BF,
∴DF=
AC.
| 1 |
| 2 |

∵AD⊥BC,
∴∠ADB=90°,
∵∠ABC=45°,
∴∠BAD=45°,
∴∠ABD=∠BAD,
∴AD=BD,
∵∠ADC=90°,∠ACB=60°,
∴∠DAC=30°,
∵BE⊥AC,
∴∠AEB=90°,
∴∠AFE=90°-30°=60°,
∴∠BFD=∠AFE=60°,
∴∠ACD=∠BFD,
在△BFD和△ACD中,∠ACD=∠BFD,∠ADC=∠BDF=90°,BD=AD,
∴△BDF≌△ACD,
∴BF=AC,
在Rt△BDF中,∠BFD=60°,那么∠DBF=30°,
∴DF=
| 1 |
| 2 |
∴DF=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定和性质、含30°角的直角三角形的性质,解题的关键是求出∠BFD=60°,进而证明△BDF≌△ACD.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
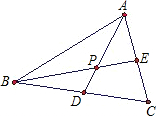 已知如图,AD、BE为△ABC的中线,且AD与BE相交于点P,若AD=6,则AP=
已知如图,AD、BE为△ABC的中线,且AD与BE相交于点P,若AD=6,则AP= 如图,AD、BE为锐角△ABC的高,若BF=AC,BC=7,CD=2,则AF的长为( )
如图,AD、BE为锐角△ABC的高,若BF=AC,BC=7,CD=2,则AF的长为( )