题目内容
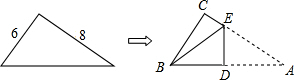 如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )分析:在Rt△BEC中利用勾股定理计算出AB=10,根据折叠的性质得到AD=BD=5,EA=EB,设AE=x,则BE=x,EC=8-x,在Rt△BEC中根据勾股定理计算出x=
,则EC=8-
=
,
利用三角形面积公式计算出S△BCE=
BC•CE=
×6×
=
,在Rt△BED中利用勾股定理计算出ED=
=
,利用三角形面积公式计算出S△BDE=
BD•DE=
×5×
=
,然后求出两面积的比.
| 25 |
| 4 |
| 25 |
| 4 |
| 7 |
| 4 |
利用三角形面积公式计算出S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
| 21 |
| 4 |
(
|
| 15 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
| 75 |
| 8 |
解答:解:在Rt△BEC中,BC=6,AC=8,
∴AB=
=10,
∵把△ABC沿DE使A与B重合,
∴AD=BD,EA=EB,
∴BD=
AB=5,
设AE=x,则BE=x,EC=8-x,
在Rt△BEC中,∵BE2=EC2+BC2,即x2=(8-x)2+62,
∴x=
,
∴EC=8-x=8-
=
,
∴S△BCE=
BC•CE=
×6×
=
,
在Rt△BED中,∵BE2=ED2+BD2,
∴ED=
=
,
∴S△BDE=
BD•DE=
×5×
=
,
∴S△BCE:S△BDE=
:
=14:25.
故选B.
∴AB=
| AC2+BC2 |
∵把△ABC沿DE使A与B重合,
∴AD=BD,EA=EB,
∴BD=
| 1 |
| 2 |
设AE=x,则BE=x,EC=8-x,
在Rt△BEC中,∵BE2=EC2+BC2,即x2=(8-x)2+62,
∴x=
| 25 |
| 4 |
∴EC=8-x=8-
| 25 |
| 4 |
| 7 |
| 4 |
∴S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
| 21 |
| 4 |
在Rt△BED中,∵BE2=ED2+BD2,
∴ED=
(
|
| 15 |
| 4 |
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
| 75 |
| 8 |
∴S△BCE:S△BDE=
| 21 |
| 4 |
| 75 |
| 8 |
故选B.
点评:本题考查了折叠问题:折叠前后两图形全等,即对应线段相等,对应角相等.也考查了勾股定理.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
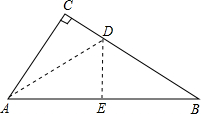 如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8,折叠△ABC的一角,使点B与点A重合,展开得折痕DE,求BD的长.
如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8,折叠△ABC的一角,使点B与点A重合,展开得折痕DE,求BD的长.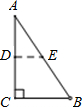 8、如图,直角三角形纸片ABC的∠C为90°,将三角形纸片沿着图示的中位线DE剪开,然后把剪开的两部分重新拼接成不重叠的图形,下列选项中不能拼出的图形是( )
8、如图,直角三角形纸片ABC的∠C为90°,将三角形纸片沿着图示的中位线DE剪开,然后把剪开的两部分重新拼接成不重叠的图形,下列选项中不能拼出的图形是( )
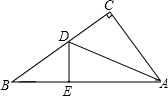 如图,直角三角形纸片的两直角边AC=6cm,BC=8cm.现将直角边AC沿AD折叠,使它落在斜边AB上,点C与点E重合.求CD的长.
如图,直角三角形纸片的两直角边AC=6cm,BC=8cm.现将直角边AC沿AD折叠,使它落在斜边AB上,点C与点E重合.求CD的长.