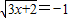题目内容
下列一元或二元的方程中没有实数解的是
- A.3x+2y=-1
- B.
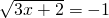
- C.3x2+2y2=-1
- D.3x2+2x=-1
BCD
分析:由二元一次方程有无数组解可对A进行判断;对于B,方程左边为非负数,而方程右边为负数,由此得到原方程无实数根;对于C,由于3x2≥0,2y2≥0,得到方程左边大于或等于0,而方程右边为负数,由此得到原方程无实数根;对于D,先化为一般式得到3x2+2x+1=0,再计算△,得到△=4-4×3×1<0,由此得到方程无实数根.
解答:A、二元一次方程有无数组解,所以A选项不正确;
B、方程左边为非负数,方程右边为负数,则原方程无实数根,所以B选项正确;
C、因为3x2≥0,2y2≥0,得到方程左边大于或等于0,不可能等于-1,原方程无实数根,所以C选项正确;
D、方程变形3x2+2x+1=0,因为△=4-4×3×1<0,则此方程无实数根,所以D选项正确.
故选B、C、D.
点评:本题考查了无理方程:根号内含有未知数的方程叫无理方程;解无理方程的基本思想是把无理方程转化为有理方程来解,常常采用平方法去根号.也考查了一元二次方程的判别式.
分析:由二元一次方程有无数组解可对A进行判断;对于B,方程左边为非负数,而方程右边为负数,由此得到原方程无实数根;对于C,由于3x2≥0,2y2≥0,得到方程左边大于或等于0,而方程右边为负数,由此得到原方程无实数根;对于D,先化为一般式得到3x2+2x+1=0,再计算△,得到△=4-4×3×1<0,由此得到方程无实数根.
解答:A、二元一次方程有无数组解,所以A选项不正确;
B、方程左边为非负数,方程右边为负数,则原方程无实数根,所以B选项正确;
C、因为3x2≥0,2y2≥0,得到方程左边大于或等于0,不可能等于-1,原方程无实数根,所以C选项正确;
D、方程变形3x2+2x+1=0,因为△=4-4×3×1<0,则此方程无实数根,所以D选项正确.
故选B、C、D.
点评:本题考查了无理方程:根号内含有未知数的方程叫无理方程;解无理方程的基本思想是把无理方程转化为有理方程来解,常常采用平方法去根号.也考查了一元二次方程的判别式.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目