题目内容
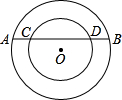 如图,同心圆中,大圆的弦AB交小圆于C,D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为( )
如图,同心圆中,大圆的弦AB交小圆于C,D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为( )| A、3:2 | ||||
B、
| ||||
C、
| ||||
| D、5:4 |
分析:过O点作OE⊥AB,E点为垂足,连OC,OA,则OE=1,而AB=4,CD=2,由垂径定理得到CE=1,AE=2,在Rt△OCE中和在Rt△OAE中,分别利用勾股定理求出OC,OA,然后计算它们的比值即可.
解答: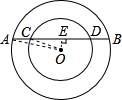 解:过O点作OE⊥AB,E点为垂足,连OC,OA,如图,
解:过O点作OE⊥AB,E点为垂足,连OC,OA,如图,
则OE=1,
∵OE⊥AB,
∴CE=DE,AE=BE,
而AB=4,CD=2,
∴CE=1,AE=2,
在Rt△OCE中,OC=
=
=
;
在Rt△OAE中,OA=
=
=
;
∴OC:OA=
:
,
即两个同心圆的半径之比为
:
.
故选C.
 解:过O点作OE⊥AB,E点为垂足,连OC,OA,如图,
解:过O点作OE⊥AB,E点为垂足,连OC,OA,如图,则OE=1,
∵OE⊥AB,
∴CE=DE,AE=BE,
而AB=4,CD=2,
∴CE=1,AE=2,
在Rt△OCE中,OC=
| OE2+CE2 |
| 12+12 |
| 2 |
在Rt△OAE中,OA=
| OE2+AE2 |
| 12+22 |
| 5 |
∴OC:OA=
| 2 |
| 5 |
即两个同心圆的半径之比为
| 2 |
| 5 |
故选C.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.

练习册系列答案
相关题目
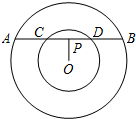
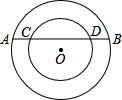 如图,同心圆中,大圆的弦AB交小圆于C,D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为
如图,同心圆中,大圆的弦AB交小圆于C,D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为 :2
:2
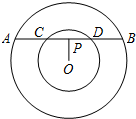

 :2
:2 :
: