题目内容
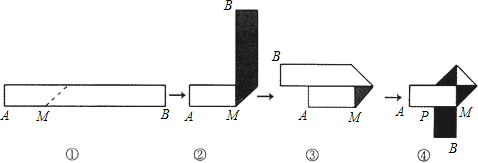
生活中，有人喜欢把传送的便条折成
形状，折叠过程是这样的（阴影部分表示纸条的反面）：
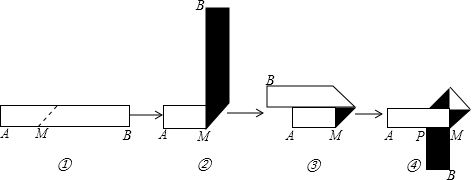
如果由信纸折成的长方形纸条（图①）长为25cm，宽为x cm，为了保证能折成图④的形状（即纸条两端均超出点P），那么x的取值范围是
分析：立体图形问题可以转化为平面图形问题解决．将图形展开我们可看到，超出P点的线段有两条与x相等，还有两条是以x为边长的正方形的对角线，列出不等式解答即可．从实物出发，结合具体的问题，辨析几何体的展开图，通过结合立体图形与平面图形的转化，建立空间观念，是解决此类问题的关键．
解答：解：根据题意列不等式可得0＜2x+2
x＜25，
解得0＜x＜5．
故答案为：0＜x＜5．
| 2 |
解得0＜x＜5．
故答案为：0＜x＜5．
点评：本题主要考查展开图折叠成几何体．通过结合立体图形与平面图形的相互转化，去理解和掌握几何体的展开图，要注意多从实物出发，然后再从给定的图形中辨认它们展开以后的形状．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
，折叠过程如图所示（阴影部分表示纸条的反面）：
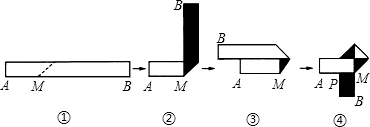
，折叠过程是这样的（阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为26cm，宽为xcm，分别回答下列问题：
