题目内容
【题目】(12分)如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF.
(1)在图中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置;
(2)线段BE与DF有什么关系?证明你的结论.

【答案】(1)见解析;
【解析】试题分析:(1)利用正方形的性质得到∠BAD=90°,而△ABE≌△ADF,则利用旋转的定义可将△ABE绕点A逆时针旋转90°可得到△ADF;
(2)利用全等三角形的性质可得BE=DF,ABE=∠ADF,则利用对顶角相等和三角形内角和可判断∠DHE=∠EAB=90°,从而得到BE⊥DF.
试题解析:(1)把△ABE绕点A逆时针旋转90°可得到△ADF;
(2)BE=DF,BE⊥DF.理由如下:
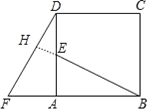
∵△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
而∠AEB=∠DEH,
∴∠DHE=∠EAB=90°,
∴BE⊥DF.

练习册系列答案
相关题目