Question

（2012•东莞模拟）如图，已知△ABC中，AB=AC，
（1）请用尺规作图的方法找出线段BC的中点，
（2）若AB边长为6，∠B=30°，求△ABC的面积．

Answer 1

分析：（1）作出BC的垂直平分线交点为D即是BC中点；
（2）作AD⊥BC，构造直角△ABD，利用“30°的角所对的直角边是斜边的一半”求出AD，BD的长，再利用三角形的面积公式解答．

解答：解：（1）如图所示：
；

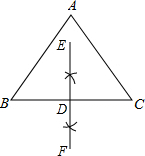（2）如图所示，作AD⊥BC于点D：

∵AB边长为6，∠B=30°，
∴AD=

1

2

×6=3，
∴BD=

62-32

=3

3

，则BC=6

3

，
∴△ABC的面积为：

1

2

×3×6

3

=9

3

．

点评：此题主要考查了复杂作图以及含30°角的直角三角形，关键是根据题意，构造直角三角形，利用30°的角所对的直角边是斜边的一半解答．