题目内容
如图1,已知梯形ABCD中,AD∥BC,AB=10,BC=12,cosB=| 3 | 5 |
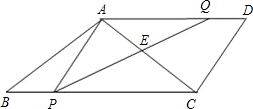 BC上移动(点P不与点B、C重合),点Q在射线AD上移动,且在移动的过程中始终有∠APQ=∠CAD,PQ交AC于点E.
BC上移动(点P不与点B、C重合),点Q在射线AD上移动,且在移动的过程中始终有∠APQ=∠CAD,PQ交AC于点E.(1)求对角线AC的长;
(2)若PB=4,求AE的长;
(3)当△APE为等腰三角形时,求PB的长.
分析:(1)作AH⊥BC,垂足为H.在直角三角形ABH中,利用余弦三角函数的定义求得BH=6,所以HC=6;然后在Rt△AHC中,由勾股定理求得AC的长度;
(2)先证明△ABP∽△PCE,然后由相似三角形的对应边成比例求得CE的长度,从而求得AE=AB-CE=10-3.2=6.8;
(3)由△APE∽△ACP推知,当△APE是等腰三角形时,△ACP也一定是等腰三角形.所以应该分类讨论:①当PC=AC=10时,PB=BC-PC=BC-AB;②当PA=PC时,△ACP∽△BCA③当AC=AP时,AE≠AP.
(2)先证明△ABP∽△PCE,然后由相似三角形的对应边成比例求得CE的长度,从而求得AE=AB-CE=10-3.2=6.8;
(3)由△APE∽△ACP推知,当△APE是等腰三角形时,△ACP也一定是等腰三角形.所以应该分类讨论:①当PC=AC=10时,PB=BC-PC=BC-AB;②当PA=PC时,△ACP∽△BCA③当AC=AP时,AE≠AP.
解答: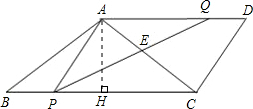 解:(1)作AH⊥BC,垂足为H(1分).
解:(1)作AH⊥BC,垂足为H(1分).
在Rt△ABH中,∵cosB=
,
∴BH=ABcosB=10×
=6,
∴HC=BC-BH=12-6=6(1分)
∴AH=
=
=8,
在Rt△AHC中,由勾股定理得AC=
=
=10(1分)
(2)∵AB=10,Ac=10,
∴AB=AC,
∴∠B=∠ACB,
∵AD∥BC,得∠CAD=∠ACB,
∵∠APQ=∠CAD,
∴∠APQ=∠ACB,
∴∠B=∠ACB=∠APQ.
∵∠APC=∠B+∠BAP=∠APQ+∠QPC,
又∵∠APQ=∠B,∴∠BAP=∠QPC,
即∠BAP=∠EPC(2分)
又∵∠B=∠ACB∴△ABP∽△PCE,
∴
=
(1分),即
=
解得CE=3.2
∴AE=AB-CE=10-3.2=6.8(2分)
(3)∵∠APQ=∠ACB,即∠APE=∠ACB
又∵∠PAE=∠PAC
∴△APE∽△ACP(1分)
∴当△APE是等腰三角形时,△ACP也一定是等腰三角形.
①当PC=AC=10时,PB=BC-PC=BC-AB=12-10=2(1分).
②当PA=PC时,∠PAC=∠PCA=∠ABC,∴△ACP∽△BCA(1分).
∴
=
∴AC2=PC•BC,即102=12PC,解得PC=
∴PB=
(1分).
③当AC=AP时,则有∠APC=∠ACB=∠ABC,
∵点P在BC边上,∴点P与点B重合,
这与点P不与点B重合矛盾.
所以AC≠AP(1分).
综上所述,当△APE是等腰三角形时,PB=2或PB=
(1分).
 解:(1)作AH⊥BC,垂足为H(1分).
解:(1)作AH⊥BC,垂足为H(1分).在Rt△ABH中,∵cosB=
| BH |
| AB |
∴BH=ABcosB=10×
| 3 |
| 5 |
∴HC=BC-BH=12-6=6(1分)
∴AH=
| AB2-BH2 |
| 102-62 |
在Rt△AHC中,由勾股定理得AC=
| AH2+HC2 |
| 82+62 |
(2)∵AB=10,Ac=10,
∴AB=AC,
∴∠B=∠ACB,
∵AD∥BC,得∠CAD=∠ACB,
∵∠APQ=∠CAD,
∴∠APQ=∠ACB,
∴∠B=∠ACB=∠APQ.
∵∠APC=∠B+∠BAP=∠APQ+∠QPC,
又∵∠APQ=∠B,∴∠BAP=∠QPC,
即∠BAP=∠EPC(2分)
又∵∠B=∠ACB∴△ABP∽△PCE,
∴
| PB |
| AB |
| CE |
| PC |
| 4 |
| 10 |
| CE |
| 12-4 |
∴AE=AB-CE=10-3.2=6.8(2分)
(3)∵∠APQ=∠ACB,即∠APE=∠ACB
又∵∠PAE=∠PAC
∴△APE∽△ACP(1分)
∴当△APE是等腰三角形时,△ACP也一定是等腰三角形.
①当PC=AC=10时,PB=BC-PC=BC-AB=12-10=2(1分).
②当PA=PC时,∠PAC=∠PCA=∠ABC,∴△ACP∽△BCA(1分).
∴
| AC |
| PC |
| BC |
| AC |
| 25 |
| 3 |
| 11 |
| 3 |
③当AC=AP时,则有∠APC=∠ACB=∠ABC,
∵点P在BC边上,∴点P与点B重合,
这与点P不与点B重合矛盾.
所以AC≠AP(1分).
综上所述,当△APE是等腰三角形时,PB=2或PB=
| 11 |
| 3 |
点评:本题综合考查了相似三角形的判定与性质、梯形、解直角三角形、勾股定理等几何知识.注意,解答(3)时,要分类讨论,以防漏解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目


 (3)在图1中,设点D坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、
(3)在图1中,设点D坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、
