题目内容
关于函数y1=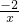 与y2=x2+2的说法(1)两图象只有一个交点,(2)当x<0时,y1>y2,(3)当x>0时,两函数的值都随x的增大而增大,(4)两函数图象的对称轴都是y轴,其中错误的个数是
与y2=x2+2的说法(1)两图象只有一个交点,(2)当x<0时,y1>y2,(3)当x>0时,两函数的值都随x的增大而增大,(4)两函数图象的对称轴都是y轴,其中错误的个数是
- A.1
- B.2
- C.3
- D.4
B
分析:根据函数y1=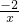 系数k=-2<0,反比例函数的图象在二、四象限,在各个象限内y随x的增大而增大,对称轴为y=x,而二次函数y2=x2+2图象位于第一、二象限,对称轴为y轴,当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大,据此进行解题.
系数k=-2<0,反比例函数的图象在二、四象限,在各个象限内y随x的增大而增大,对称轴为y=x,而二次函数y2=x2+2图象位于第一、二象限,对称轴为y轴,当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大,据此进行解题.
解答:由函数y1=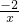 的图象位于二、四象限,而二次函数y2=x2+2的图象位于一、二象限,故两图象在第二象限有一交点,故(1)正确,
的图象位于二、四象限,而二次函数y2=x2+2的图象位于一、二象限,故两图象在第二象限有一交点,故(1)正确,
当x<时,两函数在第二象限有交点,故(2)错误,
当x>0时,两函数的值都随x的增大而增大,故(3)正确,
函数y1=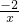 的对称轴为y=x,二次函数y2=x2+2的对称轴为y轴,故(4)错误,
的对称轴为y=x,二次函数y2=x2+2的对称轴为y轴,故(4)错误,
故正确的说法有(1)(3),
故选B.
点评:本题主要考查二次函数和反比例函数的性质的知识点,解答本题的关键是熟练掌握各类函数的性质,熟练掌握二次函数与反比例函数的交点问题和函数增减性等问题,此题综合性较强.
分析:根据函数y1=
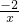 系数k=-2<0,反比例函数的图象在二、四象限,在各个象限内y随x的增大而增大,对称轴为y=x,而二次函数y2=x2+2图象位于第一、二象限,对称轴为y轴,当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大,据此进行解题.
系数k=-2<0,反比例函数的图象在二、四象限,在各个象限内y随x的增大而增大,对称轴为y=x,而二次函数y2=x2+2图象位于第一、二象限,对称轴为y轴,当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大,据此进行解题.解答:由函数y1=
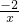 的图象位于二、四象限,而二次函数y2=x2+2的图象位于一、二象限,故两图象在第二象限有一交点,故(1)正确,
的图象位于二、四象限,而二次函数y2=x2+2的图象位于一、二象限,故两图象在第二象限有一交点,故(1)正确,当x<时,两函数在第二象限有交点,故(2)错误,
当x>0时,两函数的值都随x的增大而增大,故(3)正确,
函数y1=
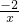 的对称轴为y=x,二次函数y2=x2+2的对称轴为y轴,故(4)错误,
的对称轴为y=x,二次函数y2=x2+2的对称轴为y轴,故(4)错误,故正确的说法有(1)(3),
故选B.
点评:本题主要考查二次函数和反比例函数的性质的知识点,解答本题的关键是熟练掌握各类函数的性质,熟练掌握二次函数与反比例函数的交点问题和函数增减性等问题,此题综合性较强.

练习册系列答案
相关题目
 与y2=x2+2的说法(1)两图象只有一个交点,(2)当x<0时,y1>y2,(3)当x>0时,两函数的值都随x的增大而增大,(4)两函数图象的对称轴都是y轴,其中错误的个数是( )
与y2=x2+2的说法(1)两图象只有一个交点,(2)当x<0时,y1>y2,(3)当x>0时,两函数的值都随x的增大而增大,(4)两函数图象的对称轴都是y轴,其中错误的个数是( )