题目内容
 已知:如图,△ABC中,AB=4,D是AB边上的一个动点,DE∥BC,连接DC,设△ABC的面积为S,△DCE的面积为S′.
已知:如图,△ABC中,AB=4,D是AB边上的一个动点,DE∥BC,连接DC,设△ABC的面积为S,△DCE的面积为S′.
(1)当D为AB边的中点时,求S′:S的值;
(2)若设AD=x,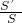 =y,试求y与x之间的函数关系式及x的取值范围.
=y,试求y与x之间的函数关系式及x的取值范围.
解:过A作AM⊥BC,交DE于点N,设AD=x,
根据DE∥BC,可以得到 =
= =
= =
= ,
,
则DE= •BC,AN=
•BC,AN= •AM;
•AM;
(1)当D为AB中点时,DE是三角形ABC的中位线,
则DE= BC,AN=
BC,AN= AM,而S△ABC=S=
AM,而S△ABC=S= •AM•BC,
•AM•BC,
∴S△DEC=S′= •AN•DE,
•AN•DE,
∴S1:S的值是1:4;
(2)作AM⊥BC,垂足为M,交DE于N点,
∵DE∥BC,∴△ADE∽△ABC,
∴ =
= =
= =
= ,
,
∴ =
= ,
,
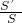 =(
=( •MN•DE):(
•MN•DE):( •AM•BC)=
•AM•BC)= •
• =
= •
• =
=
即y=- +
+ x,(0<x<4).
x,(0<x<4).
分析:(1)当D为AB中点时,DE是三角形ABC的中位线,DE:BC=1:2,而高线的比也是1:2,则三角形的面积的比就可以求出;
(2)根据相似三角形的性质,可以得到底边DE、BC以及高线之间的关系,就可以求出面积的比.
点评:本题主要考查了相似三角形的性质以及三角形的面积的计算方法.正确表示出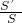 =
= •
• 是解题关键.
是解题关键.

根据DE∥BC,可以得到
 =
= =
= =
= ,
,则DE=
 •BC,AN=
•BC,AN= •AM;
•AM;(1)当D为AB中点时,DE是三角形ABC的中位线,
则DE=
 BC,AN=
BC,AN= AM,而S△ABC=S=
AM,而S△ABC=S= •AM•BC,
•AM•BC,∴S△DEC=S′=
 •AN•DE,
•AN•DE,∴S1:S的值是1:4;
(2)作AM⊥BC,垂足为M,交DE于N点,
∵DE∥BC,∴△ADE∽△ABC,
∴
 =
= =
= =
= ,
,∴
 =
= ,
,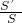 =(
=( •MN•DE):(
•MN•DE):( •AM•BC)=
•AM•BC)= •
• =
= •
• =
=
即y=-
 +
+ x,(0<x<4).
x,(0<x<4).分析:(1)当D为AB中点时,DE是三角形ABC的中位线,DE:BC=1:2,而高线的比也是1:2,则三角形的面积的比就可以求出;
(2)根据相似三角形的性质,可以得到底边DE、BC以及高线之间的关系,就可以求出面积的比.
点评:本题主要考查了相似三角形的性质以及三角形的面积的计算方法.正确表示出
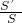 =
= •
• 是解题关键.
是解题关键. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.