题目内容
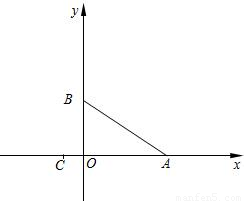
(2010•松江区二模)如图,在平面直角坐标系中,直线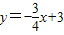 分别与x轴、y轴交于点A和点B,二次函数y=ax2-4ax+c的图象经过点B和点C(-1,0),顶点为P.
分别与x轴、y轴交于点A和点B,二次函数y=ax2-4ax+c的图象经过点B和点C(-1,0),顶点为P.(1)求这个二次函数的解析式,并求出P点坐标;
(2)若点D在二次函数图象的对称轴上,且AD∥BP,求PD的长;
(3)在(2)的条件下,如果以PD为直径的圆与圆O相切,求圆O的半径.
【答案】分析:(1)根据已知直线的解析式,可求得A、B的坐标,然后将B、C的坐标代入抛物线的解析式中,即可求得待定系数的值,从而确定该抛物线的解析式;利用配方法将所得抛物线解析式化为顶点坐标式,进而可求得顶点P的坐标;
(2)由(1)的P点坐标知:抛物线的对称轴为x=2,因此抛物线对称轴经过AB的中点,设此交点为E,若BP∥AD,那么PE=DE,根据抛物线的对称轴方程易求得E点坐标,从而可得到PE的长,根据PD=2PE即可得解;
(3)由(2)知E是PD的中点,OE的长易求得,比较ED、OE的大小后发现,DE>OE,若⊙E、⊙O相切,那么只有内切一种情况,故两圆的半径差等于圆心距,由此求得⊙O的半径.
解答:解:(1)因为直线 分别与x轴、y轴交于点A和点B;
分别与x轴、y轴交于点A和点B;
由x=0,得y=3,y=0,得x=4,
所以A(4,0),B(0,3);
把C(-1,0),B(0,3)代入y=ax2-4ax+c中,
得 ,
,
解得 ;
;
∴这个二次函数的解析式为 ;
;
 ,P点坐标为P
,P点坐标为P ;
;
(2)设二次函数图象的对称轴与直线 交于E点,与x轴交于F点;
交于E点,与x轴交于F点;
把x=2代入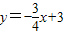
得,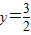 ,
,
∴ ,
,
∴ ;
;
∵PE∥OB,OF=AF,
∴BE=AE,
∵AD∥BP,
∴PE=DE,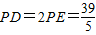 ;
;
(3)∵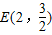 ,
,
∴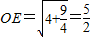 ,
,
∴ED>OE;
设圆O的半径为r,以PD为直径的圆与圆O相切时,只有内切,
∴| -r|=
-r|= ,
,
解得: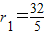 ,
, ,
,
即圆O的半径为 或
或 .
.
点评:此题考查了二次函数解析式的确定、函数图象交点坐标的求法、圆与圆的位置关系等知识,难度适中.
(2)由(1)的P点坐标知:抛物线的对称轴为x=2,因此抛物线对称轴经过AB的中点,设此交点为E,若BP∥AD,那么PE=DE,根据抛物线的对称轴方程易求得E点坐标,从而可得到PE的长,根据PD=2PE即可得解;
(3)由(2)知E是PD的中点,OE的长易求得,比较ED、OE的大小后发现,DE>OE,若⊙E、⊙O相切,那么只有内切一种情况,故两圆的半径差等于圆心距,由此求得⊙O的半径.
解答:解:(1)因为直线
 分别与x轴、y轴交于点A和点B;
分别与x轴、y轴交于点A和点B;由x=0,得y=3,y=0,得x=4,
所以A(4,0),B(0,3);
把C(-1,0),B(0,3)代入y=ax2-4ax+c中,
得
 ,
,解得
 ;
;∴这个二次函数的解析式为
 ;
; ,P点坐标为P
,P点坐标为P ;
;(2)设二次函数图象的对称轴与直线
 交于E点,与x轴交于F点;
交于E点,与x轴交于F点;把x=2代入
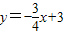
得,
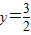 ,
,∴
 ,
,∴
 ;
;∵PE∥OB,OF=AF,
∴BE=AE,
∵AD∥BP,
∴PE=DE,
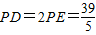 ;
;(3)∵
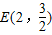 ,
,∴
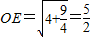 ,
,∴ED>OE;
设圆O的半径为r,以PD为直径的圆与圆O相切时,只有内切,
∴|
 -r|=
-r|= ,
,解得:
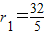 ,
, ,
,即圆O的半径为
 或
或 .
.点评:此题考查了二次函数解析式的确定、函数图象交点坐标的求法、圆与圆的位置关系等知识,难度适中.

练习册系列答案
相关题目
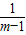 -
-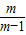 = .
= .