题目内容
已知⊙O的半径OA=2,弦AB,AC的长分别是2 ,2
,2 ,则∠BAC的度数为
,则∠BAC的度数为
- A.15°
- B.75°
- C.15°或75°
- D.15°或45°
C
分析:根据圆的轴对称性知有两种情况:两弦在圆心的同旁;两弦在圆心的两旁.
根据垂径定理和三角函数求解.
解答: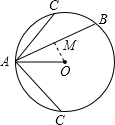 解:过点O作OM⊥AB于M,
解:过点O作OM⊥AB于M,
在直角△AOM中,OA=2.根据OC⊥AB,则AM= AB=
AB= ,
,
所以cos∠OAM= ,则∠OAM=30°,
,则∠OAM=30°,
同理可以求出∠OAC=45°,
当AB,AC位于圆心的同侧时,∠BAC的度数为45-30=15°;
当AB,AC位于圆心的异侧时,∠BAC的度数为45+30=75°.
故选C.
点评:分类讨论是此题的关键.
分析:根据圆的轴对称性知有两种情况:两弦在圆心的同旁;两弦在圆心的两旁.
根据垂径定理和三角函数求解.
解答:
 解:过点O作OM⊥AB于M,
解:过点O作OM⊥AB于M,在直角△AOM中,OA=2.根据OC⊥AB,则AM=
 AB=
AB= ,
,所以cos∠OAM=
 ,则∠OAM=30°,
,则∠OAM=30°,同理可以求出∠OAC=45°,
当AB,AC位于圆心的同侧时,∠BAC的度数为45-30=15°;
当AB,AC位于圆心的异侧时,∠BAC的度数为45+30=75°.
故选C.
点评:分类讨论是此题的关键.

练习册系列答案
相关题目
已知⊙O的半径OA=10cm,弦AB=16cm,P为弦AB上的一个动点,则OP的最短距离为( )
| A、5cm | B、6cm | C、8cm | D、10cm |
 如图,已知⊙O的半径OA=
如图,已知⊙O的半径OA= 如图,已知⊙O的半径OA=6,B为⊙O上一点,∠ABC=45°,则∠AOC所对的弧AC的长为
如图,已知⊙O的半径OA=6,B为⊙O上一点,∠ABC=45°,则∠AOC所对的弧AC的长为 (2013•来宾)如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是
(2013•来宾)如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是