题目内容
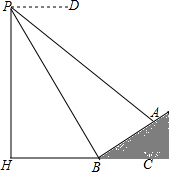 (2013•赤峰)如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC=
(2013•赤峰)如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC=
| ||
| 3 |
(1)求∠ABP的度数;
(2)求A,B两点间的距离.
分析:(1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
解答:解:(1)∵tan∠ABC=
,
∴∠ABC=30°;
∵从P点望山脚B处的俯角60°,
∴∠PBH=60°,
∴∠ABP=180°-30°-60°=90°
(2)由题意得:∠PBH=60°,
∵∠ABC=30°,
∴∠ABP=90°,
又∵∠APB=30°,
∴△PAB为直角三角形,
在直角△PHB中,PB=PH÷sin∠PBH=200
(m).
在直角△PBA中,AB=PB•tan∠BPA=200(m).
∴A、B两点之间的距离为200米.
| ||
| 3 |
∴∠ABC=30°;
∵从P点望山脚B处的俯角60°,
∴∠PBH=60°,
∴∠ABP=180°-30°-60°=90°
(2)由题意得:∠PBH=60°,
∵∠ABC=30°,
∴∠ABP=90°,

又∵∠APB=30°,
∴△PAB为直角三角形,
在直角△PHB中,PB=PH÷sin∠PBH=200
| 3 |
在直角△PBA中,AB=PB•tan∠BPA=200(m).
∴A、B两点之间的距离为200米.
点评:本题主要考查了俯角的问题以及坡度的定义,正确利用三角函数是解题的关键.

练习册系列答案
相关题目
 (2013•赤峰)如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABCD与S四边形ECDF的大小关系是( )
(2013•赤峰)如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABCD与S四边形ECDF的大小关系是( ) (2013•赤峰)如图所示,几何体的俯视图是( )
(2013•赤峰)如图所示,几何体的俯视图是( ) (2013•赤峰)如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为(
(2013•赤峰)如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为( (2013•赤峰)如图,矩形ABCD中,E是BC的中点,矩形ABCD的周长是20cm,AE=5cm,则AB的长为
(2013•赤峰)如图,矩形ABCD中,E是BC的中点,矩形ABCD的周长是20cm,AE=5cm,则AB的长为 (2013•赤峰)如图,在平面直角坐标系中,⊙O的半径为1,∠BOA=45°,则过A点的双曲线解析式是
(2013•赤峰)如图,在平面直角坐标系中,⊙O的半径为1,∠BOA=45°,则过A点的双曲线解析式是