题目内容
在平面直角坐标系中，点O是坐标原点，过点A（1，2）的直线y=kx+b与x轴交于点B，且S△AOB=4，则k的值是 _________ ．
k=
或-
．
解析试题分析：先表示出B点坐标为（-
，0）；再把A（1，2）代入y=kx+b得k+b=2，则b=2-k，然后根据三角形面积公式得到
|-|•2=4，即||=4，所以|
|=4，然后解方程即可,把y=0代入y=kx+b得kx+b=0，解得x=-，所以B点坐标为（-，0）,把A（1，2）代入y=kx+b得k+b=2，则b=2-k，∵S△AOB=4，
∴|-|•2=4，即||=4，所以||=4，解得k=或-．
考点：一次函数图象上点的坐标特征.
练习册系列答案
通城学典默写能手系列答案
相关题目
(x＞0)的图像上，平行四边形CEFG的边CE∶CG＝2∶3，顶点E在CD上，G在x轴上，F点在反比例函数
的图像上，则点F的坐标为________．
（n为正整数）与坐标轴围成的三角形的面积为Sn，则S1+S2+S3+…+S2012= ．
的图象与
轴的交点的横坐标等于2，则
的取值范围是________．
，4）在连接点（0，8）和点（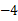
，0）的线段上，则
______.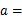