题目内容
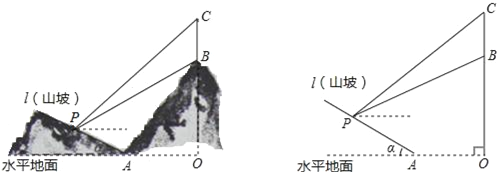
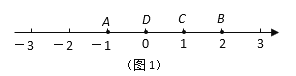
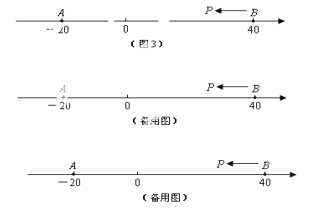
【题目】如图，在矩形ABCD中，AD＝80cm，AB＝40cm，半径为8cm的⊙O在矩形内且与AB、AD均相切．现有动点P从A点出发，在矩形边上沿着A→B→C→D的方向匀速移动，当点P到达D点时停止移动；⊙O在矩形内部沿AD向右匀速平移，移动到与CD相切时立即沿原路按原速返回，当⊙O回到出发时的位置（即再次与AB相切）时停止移动．已知点P与⊙O同时开始移动，同时停止移动（即同时到达各自的终止位置）．当⊙O到达⊙O1的位置时（此时圆心O1在矩形对角线BD上），DP与⊙O1恰好相切，此时⊙O移动了（ ）cm．
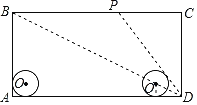
A.56B.72C.56或72D.不存在
【答案】B
【解析】
根据相同时间内速度的比等于路程的比，可得
的值，根据相似三角形的性质，可得∠ADB=∠BDP，根据等腰三角形的判定，可得BP与DP的关系，根据勾股定理，可得DP的长，根据有理数的加法，可得P点移动的距离；根据相似三角形的性质，可得
的长，分类讨论：当⊙O首次到达⊙
的位置时，当⊙O在返回途中到达⊙位置时，根据的值，可得答案．
解：存在这种情况，
设点P移动速度为v1cm/s，⊙O2移动的速度为v2cm/s，
由题意，得
，
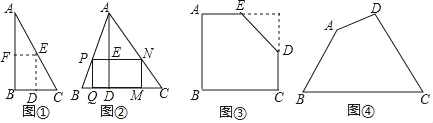
如图②：
设直线OO1与AB交于E点，与CD交于F点，⊙O1与AD相切于G点，
若PD与⊙O1相切，切点为H，则O1G＝O1H．
易得△DO1G≌△DO1H，
∴∠ADB＝∠BDP．
∵BC∥AD，
∴∠ADB＝∠CBD
∴∠BDP＝∠CBD，
∴BP＝DP．
设BP＝xcm，则DP＝xcm，PC＝（80﹣x）cm，
在Rt△PCD中，由勾股定理，得
PC2+CD2＝PD2，即（80﹣x）2+402＝x2，
解得x＝50，
此时点P移动的距离为40+50＝90cm，
∵EF∥AD，
∴△BEO1∽△BAD，
∴
，即
，
EO1＝64cm，OO1＝56cm．
①当⊙O首次到达⊙O1的位置时，⊙O移动的距离为40cm，
此时点P与⊙O移动的速度比为
，
∵
，
∴此时PD与⊙O1不能相切；
②当⊙O在返回途中到达⊙O1位置时，⊙O移动的距离为2（80﹣16）﹣56＝72cm，
∴此时点P与⊙O移动的速度比为
，
此时PD与⊙O1恰好相切，此时⊙O移动了72cm，
故选：B．
