题目内容
 (
(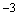 ,
,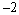 )、
)、 (2,
(2,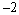 )、
)、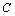 (
(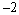 ,1)、
,1)、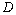 (3,1)是坐标平面内的四个点,则线段
(3,1)是坐标平面内的四个点,则线段 与
与 的关系是_________________.
的关系是_________________.
【答案】
垂直且相等
【解析】略

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
题目内容
 (
(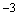 ,
,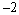 )、
)、 (2,
(2,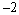 )、
)、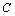 (
(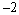 ,1)、
,1)、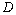 (3,1)是坐标平面内的四个点,则线段
(3,1)是坐标平面内的四个点,则线段 与
与 的关系是_________________.
的关系是_________________.
垂直且相等
【解析】略

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案