Question

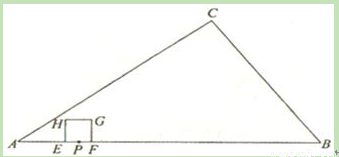
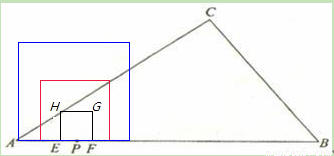
（2011•淮安）如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P在AB上，AP=2，点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立刻以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止．在点E、F运动过程中，以EF为边作正方形EFGH，使它与△ABC在线段AB的同侧．设E、F运动的时间为t/秒（t＞0），正方形EFGH与△ABC重叠部分面积为S．

（1）当时t=1时，正方形EFGH的边长是_______．当t=3时，正方形EFGH的边长是_______

（2）当0＜t≤2时，求S与t的函数关系式；

（3）直接答出：在整个运动过程中，当t为何值时，S最大？最大面积是多少？

 

Answer 1

【答案】

解：（1）当时t=1时，则PE=1，PF=1，

∴正方形EFGH的边长是2；

当t=3时，PE=1，PF=3，

∴正方形EFGH的边长是4；

（2）：①当0＜t≤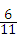时，

S与t的函数关系式是y=2t×2t=4t²；

②当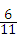＜t≤时，

S与t的函数关系式是：

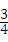y=4t²﹣[2t﹣（2﹣t）]×[2t﹣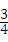（2﹣t）]，

=﹣t²+11t﹣3；

③当＜t≤2时；

S与t的函数关系式是：

y=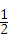（t+2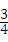）×（t+2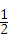）﹣（2﹣t）（2﹣t），

=3t；

（3）当t=5时，最大面积是：

s=16﹣××=；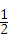

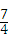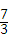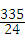【解析】略