题目内容
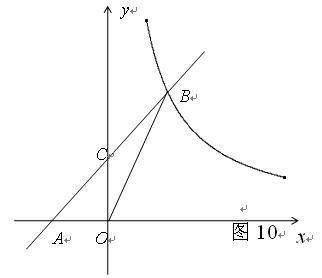
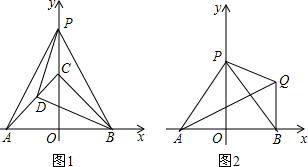
已知:如图1,在平面直角坐标系中,O为坐标原点,直线y=kx+b与x轴、y轴分别交与点A、B,与双曲线y=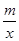 相交于C、D两点,且点D的坐标为(1,6).
相交于C、D两点,且点D的坐标为(1,6).
(1)当点C的横坐标为2时,试求直线AB的解析式,并直接写出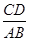 的值为 .
的值为 .
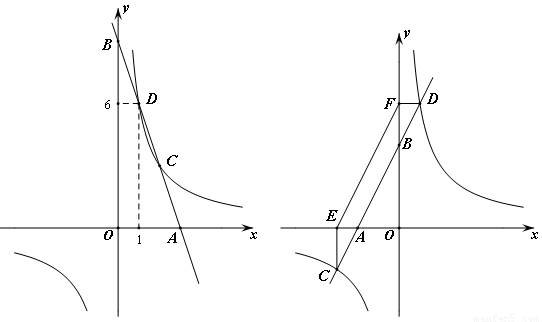
(2)如图2,当点A落在x 轴的负半轴时,过点C作x轴的垂线,垂足为E,过点D作y轴的垂线,垂足为F,连接EF.①判断ΔEFC的面积和ΔEFD的面积是否相等,并说明理由;②当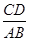 =2时,求tan∠OAB的值.
=2时,求tan∠OAB的值.
⑴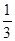 ,⑵①见解析②2
,⑵①见解析②2
【解析】(1)∵D(1,6)在y= 上,
上,
∴m=6,即双曲线解析式是 y=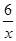 ,----------1分
,----------1分
当C点横坐标为2时,纵坐标为3,故C(2,3).
直线AB过点C(2,3),D(1,6),得
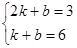 ,k=-3,b=9,故直线AB的解析式为y=-3x+9.-----3分
,k=-3,b=9,故直线AB的解析式为y=-3x+9.-----3分
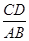 的值为
的值为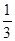 ----------------4分
----------------4分
(2)①设C(a,b),则ab=6,
∵SΔEFC=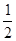 (-a)(-b)=
(-a)(-b)=
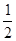 ab=3,----------------5分
ab=3,----------------5分
而SΔEFD=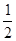 ×1×6=3,
×1×6=3,
∴SΔEFC=SΔEFD--------------------6分
②由SΔEFC=SΔEFD
知EF∥CD,易知DFEA,FBCE都是平行四边形,--------------7分
∴CE=BF,易知三角形DFB与三角形AEC全等,
∴AC=BD,-----------------9分
∵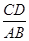 =2,设CD=2k,AB=k,DB=
=2,设CD=2k,AB=k,DB=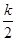 ,
,
∴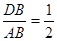 ,由ΔDFB∽ΔAOB,知OA=2,且
,由ΔDFB∽ΔAOB,知OA=2,且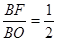 , -------10分
, -------10分
∴OB=4, ∴tan∠OAB=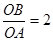 .------ ------11分
.------ ------11分
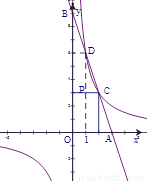
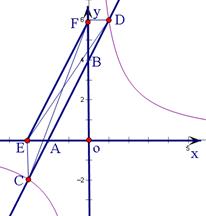
图1 图2
(1)首先由点D可求出双曲线的解析式,再由点C的横坐标为2时求出它的纵坐标,即可求出直线AB的解析式,利用勾股定理求出AB、CD的长
(2)利用C、D点的坐标,判断ΔEFC的面积和ΔEFD的面积相等;通过三角形DFB与三角形AEC全等,求得AC=BD,从而求得ΔDFB∽ΔAOB,根据相似比求得tan∠OAB的值.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案

 D为AC的中点.
D为AC的中点.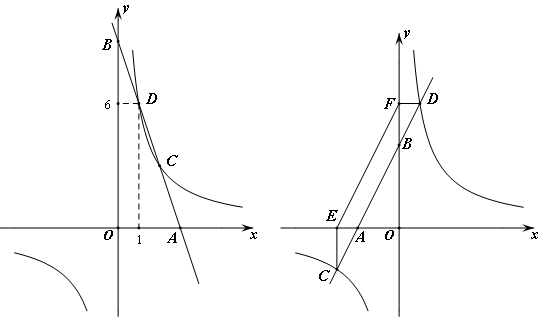
 中,直线
中,直线 与
与 轴交于点
轴交于点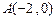 ,与反比例函数在第一象限内的图象交于点
,与反比例函数在第一象限内的图象交于点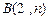 ,连结
,连结 ,若
,若 .求该反比例函数的解析式和直线
.求该反比例函数的解析式和直线