题目内容
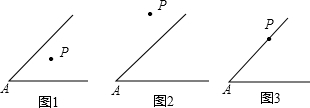 点P与∠A的位置关系如图所示.
点P与∠A的位置关系如图所示.
(1)在图1,图2,图3中,以P为顶点作出∠P(0°<∠P<90°),使∠P得两边所在的直线分别和∠A的两边垂直;
(2)量一量∠P和∠A的度数,分别写出∠P与∠A的数量关系;
在图1中,∠P=________;
在图2中,∠P=________;
在图3中,∠P=________;
(3)请你说明图2所得的结论是正确的.
解:(1)
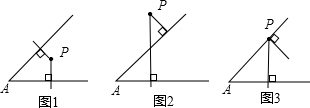 ;
;
(2)图1中∠P+∠A=180°;图2中∠P=∠A;图3中∠P=∠A;
(3)证明:在Rt△PDC中,∠DCP+∠P=90°(直角三角形的两个锐角互为余角);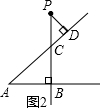
在Rt△ABC中,∠ACB+∠A=90°(直角三角形的两个锐角互为余角);
又∵∠DCP=∠ACB(对顶角相等),
∴∠P=∠A(同角的余角相等).
故答案为:(2)180°-∠A、∠A、∠A.
分析:(1)过点P作∠A两边的垂线段即可;
(2)∠P+∠A=180°;
(3)利用对顶角相等和等角的余角相等可知2中∠A=∠P.
点评:本题考查了垂线.解答此题时,利用了垂线的定义(如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足)来作以P为顶点的∠P(0°<∠P<90°)的两边所在的直线分别和∠A的两边垂直;在证明(2)的结论时,利用对顶角相等和等角的余角相等可知2中∠A=∠P.
 ;
;(2)图1中∠P+∠A=180°;图2中∠P=∠A;图3中∠P=∠A;
(3)证明:在Rt△PDC中,∠DCP+∠P=90°(直角三角形的两个锐角互为余角);

在Rt△ABC中,∠ACB+∠A=90°(直角三角形的两个锐角互为余角);
又∵∠DCP=∠ACB(对顶角相等),
∴∠P=∠A(同角的余角相等).
故答案为:(2)180°-∠A、∠A、∠A.
分析:(1)过点P作∠A两边的垂线段即可;
(2)∠P+∠A=180°;
(3)利用对顶角相等和等角的余角相等可知2中∠A=∠P.
点评:本题考查了垂线.解答此题时,利用了垂线的定义(如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足)来作以P为顶点的∠P(0°<∠P<90°)的两边所在的直线分别和∠A的两边垂直;在证明(2)的结论时,利用对顶角相等和等角的余角相等可知2中∠A=∠P.

练习册系列答案
相关题目
已知⊙O的半径为4,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为( )
| A、在圆上 | B、在圆外 | C、在圆内 | D、不确定 |