题目内容
【题目】理解:我们知道: 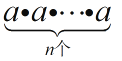 =an , am
=an , am![]() an=am+n , (am)n=
an=am+n , (am)n= 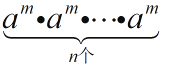 =
= ![]() =amn , 上述式子反之亦成立,请解决下列问题.
=amn , 上述式子反之亦成立,请解决下列问题.
(1)若xm+2xm+3=x9成立,求m的值;
(2)若2x=3,2y=5,求23x+2y+2的值;
(3)若2x×42x×83x=228 , 求x的值;
(4)比较2300与3200的大小.
【答案】
(1)
解:由xm+2xm+3=x9,得xm+2+m+3=x9.
由底数相同、幂相同,得m+2+m+3=9.解得m=2.
(2)
解:由2x=3,2y=5,得23x=27,22y=25,
23x+2y+2=23x×22y×22=27×25×4=2700.
(3)
解:由2x×42x×83x=228,得
2x×24x×29x=228.
2x+4x+9x=228,即x+4x+9x=28.
解得x=2.
(4)
解:2300=8100,3200=9100,
指数相同底数越大幂越大,得
2300<3200.
【解析】阅读本题材料,关键是要理解(am)n=amn;本题考查了同底数幂的乘法,(1)利用了同底数幂的乘法;(2)先化成同底数幂的幂乘法再进行同底数幂的乘法运算;(3)先化成同底数幂的幂乘法再进行同底数幂的乘法运算;(4)先化成同指数的幂,再进行同指数幂的大小比较.
【考点精析】本题主要考查了同底数幂的乘法的相关知识点,需要掌握同底数幂的乘法法则aman=am+n(m,n都是正数)才能正确解答此题.

练习册系列答案
相关题目