题目内容
已知二次函数y=x2-(m2-2)x-2m的图象与x轴交于点A(x1,0)和点B(x2,0),x1<x2,与y轴交于点C,且满足![]() +
+![]() =
=![]() .
.
(1)求这个二次函数的解析式;
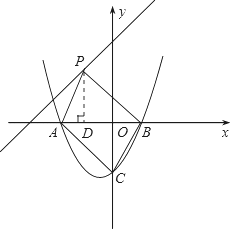
(2)探究:在直线y=x+3上是否存在一点P,使四边形PACB为平行四边形?如果有,求出点P的坐标;如果没有,请说明理由.
解析:
|
分析:(1)欲求抛物线的解析式,关键是求得m的值.根据题中所给关系式,利用一元二次方程根与系数的关系,可以求得m的值,从而问题得到解决.注意:解答中求得两个m的值,需要进行检验,把不符合题意的m值舍去; (2)利用平行四边形的性质构造全等三角形,根据全等关系求得P点的纵坐标,进而得到P点的横坐标,从而求得P点坐标. 解答:解:(1)∵二次函数y=x2-(m2-2)x-2m的图象与x轴交于点A(x1,0)和点B(x2,0),x1<x2, 令y=0,即x2-(m2-2)x-2m=0①,则有: x1+x2=m2-2,x1x2=-2m. ∴ 化简得到:m2+m-2=0,解得m1=-2,m2=1. 当m=-2时,方程①为:x2-2x+4=0,其判别式Δ=b2-4ac=-12<0,此时抛物线与x轴没有交点,不符合题意,舍去; 当m=1时,方程①为:x2+x-2=0,其判别式Δ=b2-4ac=9>0,此时抛物线与x轴有两个不同的交点,符合题意. ∴m=1, ∴抛物线的解析式为y=x2+x-2. (2)假设在直线y=x+3上是否存在一点P,使四边形PACB为平行四边形. 如图所示,连接PA.PB.AC.BC,过点P作PD⊥x轴于D点. ∵抛物线y=x2+x-2与x轴交于A.B两点,与y轴交于C点, ∴A(-2,0),B(1,0),C(0,2),∴OB=1,OC=2. ∵PACB为平行四边形,∴PA∥BC,PA=BC, ∴∠PAD=∠CBO,∴∠APD=∠OCB. 在Rt△PAD与Rt△CBO中, ∵ ∴Rt△PAD≌Rt△CBO, ∴PD=OC=2,即yP=2, ∴直线解析式为y=x+3, ∴xP=-1, ∴P(-1,2). 所以在直线y=x+3上存在一点P,使四边形PACB为平行四边形,P点坐标为(-1,2).
点评:本题是代数几何综合题,考查了二次函数的图象与性质、抛物线与x轴的交点、一元二次方程根的解法及根与系数关系、一次函数、平行四边形的性质以及全等三角形的判定与性质等方面的知识,涉及的考点较多,有一定的难度. |
提示:
|
考点:二次函数综合题. |

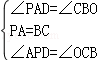 ,
,