题目内容
【题目】(1)操作发现:
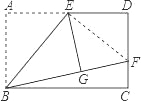
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决:
保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求:
保持(1)中条件不变,若DC=nDF,求![]() 的值.
的值.
【答案】(1)同意,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)求简单的线段相等,可证线段所在的三角形全等,即连接EF,证△EGF≌△EDF即可;
(2)可设DF=x,BC=y;进而可用x表示出DC、AB的长,根据折叠的性质知AB=BG,即可得到BG的表达式,由(1)证得GF=DF,那么GF=x,由此可求出BF的表达式,进而可在Rt△BFC中,根据勾股定理求出x、y的比例关系,即可得到![]() 的值;
的值;
(3)方法同(2).
试题解析:(1)同意,连接EF,
则根据翻折不变性得,
∠EGF=∠D=90°,EG=AE=ED,EF=EF,
在Rt△EGF和Rt△EDF中,
![]()
∴Rt△EGF≌Rt△EDF(HL),
∴GF=DF;
(2)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=2DF,
∴CF=x,DC=AB=BG=2x,
∴BF=BG+GF=3x;
在Rt△BCF中,BC2+CF2=BF2,即y2+x2=(3x)2
∴y=2![]() x,
x,
∴![]() ;
;
(3)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=nDF,
∴BF=BG+GF=(n+1)x
在Rt△BCF中,BC2+CF2=BF2,即y2+[(n-1)x]2=[(n+1)x]2
∴y=2x![]() ,
,
∴![]() .
.

【题目】小刚想买双好的运动鞋,于是他上网查找有关资料,得到下表:
颜色 | 价格(元) | 备注 | |
甲 | 红、白、蓝、灰 | 450 | 不宜在雨中穿 |
乙 | 淡黄、浅绿、白、黑 | 700 | 有很好的防水性 |
丙 | 灰、白蓝相间 | 350 | 较为防水 |
丁 | 浅绿、淡黄、白蓝相间 | 500 | 防水性很好 |
他想买一双价格在300~600元之间,白蓝相间、浅绿或淡黄色,并且防水性能很好的运动鞋,那么他应选( )
A. 甲 B. 乙 C. 丙 D. 丁