题目内容
【题目】问题背景：已知∠EDF的顶点D在△ABC的边AB所在直线上（不与A，B重合），DE交AC所在直线于点M，DF交BC所在直线于点N，记△ADM的面积为S1 ， △BND的面积为S2 ．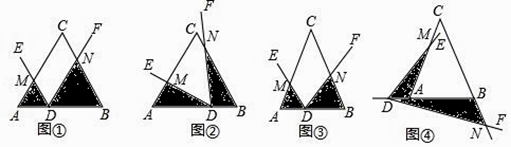 
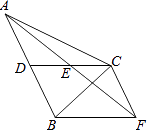
（1）初步尝试：如图①，当△ABC是等边三角形，AB=6，∠EDF=∠A，且DE∥BC，AD=2时，则S1S2=；
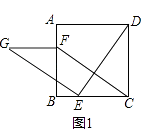
（2）类比探究：在（1）的条件下，先将点D沿AB平移，使AD=4，再将∠EDF绕点D旋转至如图②所示位置，求S1S2的值；
（3）延伸拓展：当△ABC是等腰三角形时，设∠B=∠A=∠EDF=α．
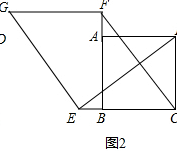
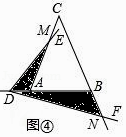
（Ⅰ）如图③，当点D在线段AB上运动时，设AD=a，BD=b，求S1S2的表达式（结果用a，b和α的三角函数表示）．
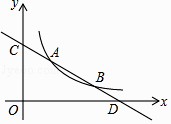
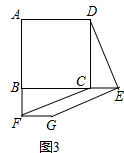
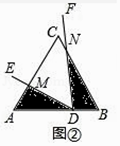
（Ⅱ）如图④，当点D在BA的延长线上运动时，设AD=a，BD=b，直接写出S1S2的表达式，不必写出解答过程．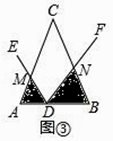
【答案】
（1）12
（2）
解：如图2中，设AM=x，BN=y．
∵∠MDB=∠MDN+∠NDB=∠A+∠AMD，∠MDN=∠A，
∴∠AMD=∠NDB，∵∠A=∠B，
∴△AMD∽△BDN，
∴ 
= 
，
∴ 
= 
，
∴xy=8，
∵S1= 
ADAMsin60°= 
x，S2= DBsin60°= 
y，
∴S1S2= x y= 
xy=12
（3）
解：Ⅰ如图3中，设AM=x，BN=y，
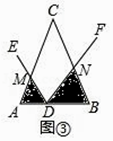
同法可证△AMD∽△BDN，可得xy=ab，
∵S1= ADAMsinα= axsinα，S2= DBBNsinα= bysinα，
∴S1S2= 
（ab）2sin2α．
Ⅱ如图4中，设AM=x，BN=y，
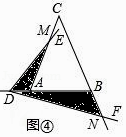
同法可证△AMD∽△BDN，可得xy=ab，
∵S1= ADAMsinα= axsinα，S2= DBBNsinα= bysinα，
∴S1S2= （ab）2sin2α．
【解析】解：（1）如图1中，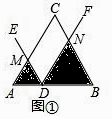
∵△ABC是等边三角形，
∴AB=CB=AC=6，∠A=∠B=60°，
∵DE∥BC，∠EDF=60°，
∴∠BND=∠EDF=60°，
∴∠BDN=∠ADM=60°，
∴△ADM，△BDN都是等边三角形，
∴S1= 
22= ，S2= （4）2=4 ，
∴S1S2=12，
所以答案是12．
【考点精析】本题主要考查了等腰三角形的性质和等边三角形的性质的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；等边三角形的三个角都相等并且每个角都是60°才能正确解答此题．
