题目内容
如图1,P为正方形ABCD内一点,且PA:PB:PC=1:2:3,求∠APB的度数.
小娜同学的想法是:不妨设PA=1,PB=2,PC=3,设法把PA、PB、PC相对集中,于是他将△BCP绕点B顺时针旋转90°得到△BAE(如图2),然后连接PE,问题得以解决.
请你回答:图2中∠APB的度数为______.
请你参考小娜同学的思路,解决下列问题:
如图3,P是等边三角形ABC内一点,已知∠APB=115°,∠BPC=125°.
(1)在图3中画出并指明以PA、PB、PC的长度为三边长的一个三角形(保留画图痕迹);
(2)求出以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等于______.

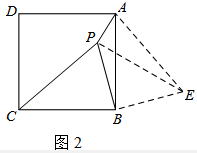 解:如图2.
解:如图2.∵根据旋转的性质知∠PBE=90°,△BCP≌△BAE.
∴BP=BE,PC=AE,
∴∠BPE=∠BEP=45°.
又PA:PB:PC=1:2:3,
∴AE2=AP2+PE2,
∴∠APE=90°,
∴∠APB=∠APE+∠BPE=90°+45°=135°,即图2中∠APB的度数为135°.
故答案是:135°;
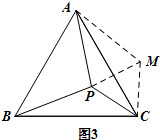
(1)如图3,将△BCP绕点C顺时针旋转60°得到△ACM,然后连接PM,△APM即为所求,即以PA、PB、PC的长度为三边长的一个三角形是△APM.以PA、PB、PC的长度为三边长的一个三角形是△APM.
(2)如图3.
∵根据旋转的性质知∠PCM=60°,△BCP≌△ACM.
∴PC=CM,∠AMC=∠BPC=125°,
∴△PCM是等边三角形,
∴∠MPC=∠PMC=60°,∠AMP=∠AMC-∠PMC=65°.
∵∠APB=115°,∠BPC=125°,∠APB+∠BPC+∠MPC+∠APM=360°,
∴∠APM=60°,
∴∠PAM=180°-∠APM-∠AMP=55°.
∴以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等于 60°、65°、55°.
故答案是:60°、65°、55°.
分析:图2中,根据旋转的性质知△BCP≌△BAE.由全等三角形的对应边相等、等腰三角形的判定推知△BPE是等腰三角形,则∠BPE=∠BEP=45°;然后由全等三角形的对应边相等、勾股定理证得∠APE=90°;最后根据图中角与角间的数量关系求得∠APB=135°;
(1)设法把PA、PB、PC相对集中,将△BCP绕点B顺时针旋转60°得到△ACM,然后连接PM,问题得以解决.
(2)根据旋转的性质知∠PCM=60°,△BCP≌△ACM.然后根据全等三角形的对应边、对应角相等,周角的定义以及三角形内角和定理来求以PA、PB、PC的长度为三边长的三角形的各内角的度数.
点评:本题综合考查了旋转的性质,等边三角形和正方形的性质以及全等三角形的判定与性质等知识点.旋转变化前后,对应角、对应线段分别相等,图形的大小、形状都不变.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
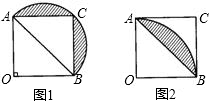 如图,四边形OBCA为正方形,图1是以AB为直径画半圆,阴影部分面积记为S1,图2是以O为圆心,OA长为半径画弧,阴影部分面积记为S2,则S1,S2的大小关系为( )
如图,四边形OBCA为正方形,图1是以AB为直径画半圆,阴影部分面积记为S1,图2是以O为圆心,OA长为半径画弧,阴影部分面积记为S2,则S1,S2的大小关系为( )| A、S1<S2 | B、S1=S2 | C、S1>S2 | D、无法判断 |

 (2013•泰安)如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=
(2013•泰安)如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=
