题目内容
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上任意一点(不与A,B重合),且CD切⊙O于点D.
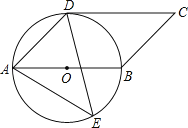
(1)试求∠AED的度数.
(2)若⊙O的半径为![]() cm,试求:△ADE面积的最大值.
cm,试求:△ADE面积的最大值.
【答案】(1)∠AED的度数为45 或135;
(2)(![]() )cm 2.
)cm 2.
【解析】
试题分析:(1)利用平行四边形的性质以及切线的性质和圆周角定理求出即可;
(2)利用当三角形高度最大时面积最大,求出EF的长即可得出答案.
解:(1)连接DO,DB,
∵四边形ABCD是平行四边形,CD切⊙O于点D.
∴DO⊥DC,
∴∠DBA=45°,
∵∠DBA=∠E,
∴∠E=45°,
当E′点在如图所示位置,即可得出∠AE′D=180°﹣45°=135°,
∴∠AED的度数为45 或135;
(2)当∠AED=45°,且E在AD垂直平分线上时,△ADE的面积最大,
∵∠AED=45°,
∴∠DAB=∠DBA=45°,∠ADB=90°,
∵⊙O的半径为![]() cm,
cm,
∴AB=6![]() cm,
cm,
∴AD=DB=6,
AF=FO=3,
∴S△ADE=![]() ×AD×(FO+EO)=
×AD×(FO+EO)=![]() ×6×(3+3
×6×(3+3![]() )=(
)=(![]() )cm 2.
)cm 2.



练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目