Question

【题目】下面是小欣设计的“利用等腰三角形做菱形”的尺规作图过程．

己知：等腰

求作：点，使得四边形为菱形．

做法：①作的角平分线，交线段于点；

②以点为圆心，长为半径圆弧，交的延长线于点；

③连接，所以四边形为菱形，点即为所求．

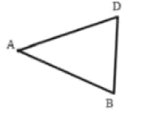
根据小新设计的尺规作图过程．

（1）使用直尺和圆规补全图形；（保留作图痕迹）

（2）完成下面的证明．

证明：平分，

（______________________________________）（填推理的依据）

∴四边形为平行四边形（______________________________________）（填推理的依据）

，

∴四边形为菱形（______________________________________）（填推理的依据）

（3）请你设计一种不同于小欣的，利用等腰（其中）作菱形的方法．

要求：写出简要思路，并尺规作图．

Answer 1

【答案】（1）见解析；（2）等腰三角形三线合一，对角线相互平分的四边形是平行四边形，对角线相互垂直的平行四边形是菱形；（3）见解析

【解析】

(1)根据要求画出图形即可；
(2)根据对角线垂直平分的四边形是菱形即可判定；

(3)根据邻边相等的平行四边形是菱形即可作出图形．

(1)如图所示，点C是所求作的点，使得四边形ABCD为菱形；

(2)∵AB=AD，AO平分∠BAD，

∴BO=DO，AC⊥BD(等腰三角形三线合一)

∵BO=DO，AO=CO，

∴四边形为平行四边形(对角线相互平分的四边形是平行四边形)

∵AC⊥BD，

∴四边形为菱形(对角线相互垂直的平行四边形是菱形)；

(3)作法：①以B为圆心，BA长为半径作弧；
②以D为圆心，DA长为半径作弧，两弧交于点C；
③连接BC、DC．

如图所示，四边形ABCD为所求作的菱形．