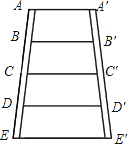
题目内容
如图所示的梯形梯子,AA'∥EE',AB=BC=CD=DE,A' B'=B' C'=C' D'=D' E', AA'=2 m, EE'=4m.求BB'、CC'、DD'的长.
答案:
解析:
提示:
解析:
|
因为 AB=BC=CD=DE,A' B'=B' C'=C' D'=D' E',AA'∥EE',所以 CC′是梯形AEE′A′的中位线.所以 CC′=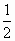 (AA′+EE′)=3 cm,CC′//AA′,CC′//EE′. (AA′+EE′)=3 cm,CC′//AA′,CC′//EE′.
由 BB′,DD′分别是梯形ACC′A′,CEE′C′的中位线,所以 BB′=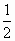 (AA′+CC′)=2.5 cm (AA′+CC′)=2.5 cm
DD′ =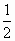 (CC′+EE′)=3.5 cm. (CC′+EE′)=3.5 cm.
所以 BB'、CC'、DD'的长分别为2.5 cm,3 cm,3.5 cm. |
提示:
|
根据条件易得, CC′是梯形AEE′A′的中位线,所以易得CC'=0.65,同理可以计算出BB′和DD′的长. |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 17、如图所示的梯形梯子,AA′∥EE′,A′B′=B′C′=C′D′=D′E′,AB=BC=CD=DE,AA′=0.4米,EE′=0.8米.求BB′、CC′、DD′的长.
17、如图所示的梯形梯子,AA′∥EE′,A′B′=B′C′=C′D′=D′E′,AB=BC=CD=DE,AA′=0.4米,EE′=0.8米.求BB′、CC′、DD′的长.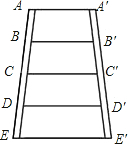 如图所示的梯形梯子,AA′∥EE′,A′B′=B′C′=C′D′=D′E′,AB=BC=CD=DE,AA′=0.4米,EE′=0.8米.求BB′、CC′、DD′的长.
如图所示的梯形梯子,AA′∥EE′,A′B′=B′C′=C′D′=D′E′,AB=BC=CD=DE,AA′=0.4米,EE′=0.8米.求BB′、CC′、DD′的长.