题目内容
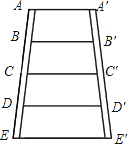
 17、如图所示的梯形梯子,AA′∥EE′,A′B′=B′C′=C′D′=D′E′,AB=BC=CD=DE,AA′=0.4米,EE′=0.8米.求BB′、CC′、DD′的长.
17、如图所示的梯形梯子,AA′∥EE′,A′B′=B′C′=C′D′=D′E′,AB=BC=CD=DE,AA′=0.4米,EE′=0.8米.求BB′、CC′、DD′的长.分析:由已知易得AA'∥BB'∥CC'∥DD'∥EE',则CC'为梯形AEE'A'的中位线,BB'为梯形ACC'A′的中位线,DD'为梯形CEE'C'的中位线,根据中位线的性质求解即可.
解答:解:∵A′B′=B′C′=C′D′=D′E′,AB=BC=CD=DE,
∴BB'∥CC'∥DD',
∵AA′∥EE′,
∴AA'∥BB'∥CC'∥DD'∥EE',
∴CC'为梯形AEE'A'的中位线,BB'为梯形ACC'A'的中位线,DD'为梯形CEE'C'的中位线,
∴CC'=(0.4+0.8)÷2=0.6,
BB'=(0.4+0.6)÷2=0.5,
DD'=(0.6+0.8)÷2=0.7.
∴BB'∥CC'∥DD',
∵AA′∥EE′,
∴AA'∥BB'∥CC'∥DD'∥EE',
∴CC'为梯形AEE'A'的中位线,BB'为梯形ACC'A'的中位线,DD'为梯形CEE'C'的中位线,
∴CC'=(0.4+0.8)÷2=0.6,
BB'=(0.4+0.6)÷2=0.5,
DD'=(0.6+0.8)÷2=0.7.
点评:此题主要考查梯形中位线的性质,以及平行线的判定,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
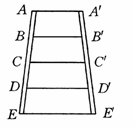
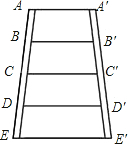 如图所示的梯形梯子,AA′∥EE′,A′B′=B′C′=C′D′=D′E′,AB=BC=CD=DE,AA′=0.4米,EE′=0.8米.求BB′、CC′、DD′的长.
如图所示的梯形梯子,AA′∥EE′,A′B′=B′C′=C′D′=D′E′,AB=BC=CD=DE,AA′=0.4米,EE′=0.8米.求BB′、CC′、DD′的长.