题目内容
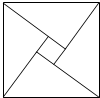 四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为49,大正方形面积为169,直角三角形中较小的锐角为θ,那么sinθ的值( )
四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为49,大正方形面积为169,直角三角形中较小的锐角为θ,那么sinθ的值( )分析:已知正方形的面积即可求出边长.根据勾股定理求出直角三角形的边长,即可求解.
解答:解:由题意知,小正方形的边长为7,大正方形的边长为13.
设直角三角形中较小的边的边长为x,
则有(7+x)2+x2=169.
解得x=5(负值不合题意,舍去)
∴sinθ=
.
故选D.
设直角三角形中较小的边的边长为x,
则有(7+x)2+x2=169.
解得x=5(负值不合题意,舍去)
∴sinθ=
| 5 |
| 13 |
故选D.
点评:此题考查了三角函数的定义和勾股定理知识点,难度中等.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 正方形.
正方形. 24、如图所示,把边长为2的正方形剪成四个全等的直角三角形,请你用这四个直角三角形拼成符合下列要求的图形各一个,并标上必要的记号:
24、如图所示,把边长为2的正方形剪成四个全等的直角三角形,请你用这四个直角三角形拼成符合下列要求的图形各一个,并标上必要的记号: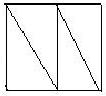 19、如图,把边长为2cm的正方形剪成四个全等的直角三角形,请用这四个直角三角形画出符合下列要求的图形(注意:四个三角形要全部用上,互不重叠且不留空隙).
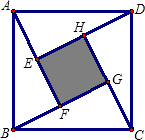
19、如图,把边长为2cm的正方形剪成四个全等的直角三角形,请用这四个直角三角形画出符合下列要求的图形(注意:四个三角形要全部用上,互不重叠且不留空隙). 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是49,小正方形的面积4,直角三角形的两直角边长分别为a,b,那么下列结论正确的有( )个.
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是49,小正方形的面积4,直角三角形的两直角边长分别为a,b,那么下列结论正确的有( )个.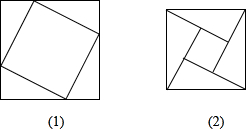 方形拼成一个大的正方形,并且两种方案中直角三角形全等,直角三角形长的直角边长为a,短的直角边长为b.
方形拼成一个大的正方形,并且两种方案中直角三角形全等,直角三角形长的直角边长为a,短的直角边长为b.