题目内容
【题目】如图，△ABC是⊙O的内接三角形，AB为⊙O直径，AB=12，AD平分∠BAC，交BC于点 E，交⊙O于点D，连接BD.
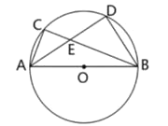
（1）求证:∠BAD=∠CBD；
（2）若∠AEB=125°，求
的长.
【答案】（1）见解析；（2）
.
【解析】
（1）根据角平分线的定义和圆周角定理即可得到结论；
（2）连接OD，根据平角定义得到∠AEC=55°，根据圆周角定理得到∠ACE=90°，求得∠CAE=35°，得到∠BOD=2∠BAD=70°，根据弧长公式即可得到结论．
（1）证明:∵AD平分∠BAC.
∴∠CAD=∠BAD
又∠CBD=∠CAD
∴∠BAD=∠CBD
（2）解: 连结OD
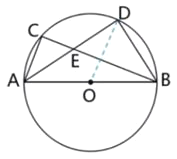
∵∠AEB=125°
∴∠AEC=55°
∵AB是直径
∴∠ACE=90°
∴∠CAE=35°，∠DAB=35°，
∴∠DOB=2∠BAD=70°
∴ 
A加金题 系列答案
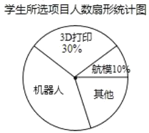
全优测试卷系列答案【题目】初一（1）班针对“你最喜爱的课外活动项目”对全班学生进行调查（每名学生分别选一个活动项目），并根据调查结果列出统计表，绘制成扇形统计图．
男、女生所选项目人数统计表
项目 | 男生（人数） | 女生（人数） |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题：
（1）m＝ ，n＝ ；
（2）扇形统计图中机器人项目所对应扇形的圆心角度数为 °；
（3）从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练，请用列举法（画树状图或列表）求所选取的2名学生中恰好有1名男生、1名女生的概率．
【题目】甲、乙两组同时加工某种零件，甲组每小时加工80件，乙组加工的零件数量y（件）与时间x（小时）为一次函数关系，部分数据如下表所示．
x（小时） | 2 | 4 | 6 |
y（件） | 50 | 150 | 250 |
（1）求y与x之间的函数关系式；
（2）甲、乙两组同时生产，加工的零件合在一起装箱，每满340件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？
