题目内容
用大小相同的小三角形摆成如图所示的图案,按照这样的规律摆放,则第n个图案中共有小三角形的个数是 .
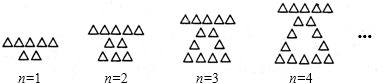
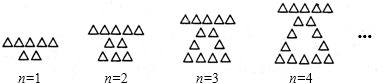
3n+4
思路分析:观察图形可知,第1个图形共有三角形5+2个;第2个图形共有三角形5+3×2-1个;第3个图形共有三角形5+3×3-1个;第4个图形共有三角形5+3×4-1个;…;则第n个图形共有三角形5+3n-1=3n+4个;
解答:解:观察图形可知,第1个图形共有三角形5+2个;
第2个图形共有三角形5+3×2-1个;
第3个图形共有三角形5+3×3-1个;
第4个图形共有三角形5+3×4-1个;
…;
则第n个图形共有三角形5+3n-1=3n+4个;故答案为:3n+4
点评:此题考查了规律型:图形的变化类,解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.

练习册系列答案
相关题目
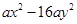 (2)
(2)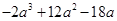
 ,其中
,其中 .
.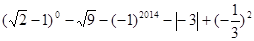 .
. ( )
( )



 收费.”若这两家旅行社的票价相同,那么( )
收费.”若这两家旅行社的票价相同,那么( )
 时,代数式
时,代数式 的值是( )
的值是( ) 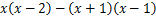 ,其中
,其中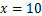 .
.