Question

【题目】在△ABC中，∠B=15°，∠C=90°，AB的垂直平分线交AB于点M，交BC于点N．已知BM=12cm，求AC的长．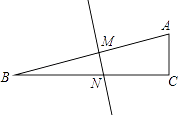

Answer 1

【答案】解：连接NA， ∵MN是线段AB的垂直平分线，
∴MA=MB=12cm，NA=NB，
∴∠MAN=∠B=15°，
∵∠ANC是△ABN的外角，
∴∠ANC=15°+15°=30°，
∴Rt△ACN中，AC= AN，
设AC=x，则AN=2x=BN，CN= x，
∵在Rt△ABC中，AC2+BC2=AB2
∴x2+（2x+ x）2=242 ，
解得x=12 ，
故AC的长为12 ．

【解析】连接NA，由MN是线段AB的垂直平分线可知，NA=NB，∠1=∠B，再根据∠2是△ABN的外角可得出∠2的度数，在Rt△ACN中根据∠2=30°可知AC= AN，根据勾股定理可得出结论．
【考点精析】根据题目的已知条件，利用线段垂直平分线的性质和勾股定理的概念的相关知识可以得到问题的答案，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．