题目内容
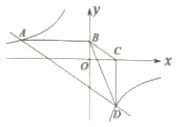
【题目】已知抛物线y=x2﹣mx﹣m﹣1与x轴交于A、B两点,点A在点B的左边,与y轴交于点C(0,﹣3).
(1)求点A、B的坐标;
(2)点D是抛物线上一点,且∠ACO+∠BCD=45°,求点D的坐标;
(3)将抛物线向上平移m个单位,交线段BC于点M,N,若∠MON=45°,求m的值.
【答案】(1)点A、B的坐标分别为:(﹣1,0)、(3,0);(2)D(![]() ,﹣
,﹣![]() )或(5,12);(3)m=
)或(5,12);(3)m=![]()
【解析】
(1)把C点的坐标代入解析式可得:﹣m﹣1=﹣3,解得:m=﹣2,即可求解;
(2)①当点D在BC下方时,∠ACO+∠BCD=45°,则AC⊥CD,则直线CD的表达式为:y=![]() x﹣3,联立①②并解得:x=0或
x﹣3,联立①②并解得:x=0或![]() ,即可求解;②当点D(D′)在BC上方时,ED的表达式为:y=﹣x+
,即可求解;②当点D(D′)在BC上方时,ED的表达式为:y=﹣x+![]() ,点H(
,点H(![]() ,﹣
,﹣![]() ),点E的坐标为:(
),点E的坐标为:(![]() ,2),即可求解;
,2),即可求解;
(3)证明△NOM∽△NCO,则NO2=MNCN,即可求解.
(1)把C(0,﹣3)代入解析式可得:﹣m﹣1=﹣3,解得:m=﹣2,
故抛物线的表达式为:y=x2﹣2x﹣3
令y=0,解得:x=3或﹣1,
故点A、B的坐标分别为:(﹣1,0)、(3,0);
(2)①当点D在BC下方时,
∵∠ACO+∠BCD=45°,则AC⊥CD,
设直线AC的解析式为y=k1x-3,代入A(﹣1,0)可得:k1=-3,
∴直线AC的解析式为y=-3x-3,
则直线CD的表达式为:y=![]() x﹣3,
x﹣3,
联立得: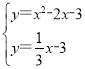 ,解得:x=0或
,解得:x=0或![]() (0舍去),
(0舍去),
故点D(![]() ,﹣
,﹣![]() );
);
②当点D(D′)在BC上方时,
过点D作DE⊥BC交BC于点H,交CD′于点E,则D点、E点关于直线BC对称,
设直线BC的解析式为y=k2x+b,把B(3,0),C(0,-3)代入得:
![]() 解得:
解得:![]()
∴直线BC的表达式为:y=x﹣3
设直线ED的表达式为:y=-x+n,把点D(![]() ,﹣
,﹣![]() )代入得:n=
)代入得:n=![]()
则ED的表达式为:y=﹣x+![]()
联立得: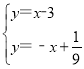 ,解得:x=
,解得:x=![]() ,故点H(
,故点H(![]() ,﹣
,﹣![]() ),根据中点坐标公式可求得点E的坐标为:(
),根据中点坐标公式可求得点E的坐标为:(![]() ,﹣
,﹣![]() ),
),
设直线CE的表达式为y=ax+c,可得 ,解得
,解得![]()
则直线CE的表达式为:y=3x﹣3
联立得: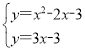 ,解得:x=0或5(0舍去),
,解得:x=0或5(0舍去),
故点D(D′)的坐标为:(5,12),
综上,点D的坐标为:(![]() ,﹣
,﹣![]() )或(5,12);
)或(5,12);
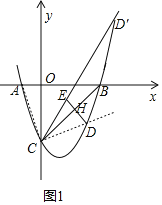
(3)如图2,抛物线平移后的图象为虚线部分,
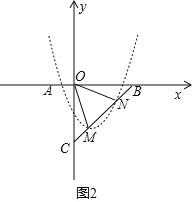
则抛物线的表达式为:y=x2﹣2x﹣3+m(m>0),
则x2﹣2x﹣3+m=x-3,
∴x2﹣3x+m=0,
设点M、N的坐标分别为:(x1,y1)、(x2、y2),
则x1+x2=3,x1x2=m,x2=![]() ,
,
∵∠MON=45°=∠OCM,∠ONM=∠ONM,
∴△NOM∽△NCO,
∴NO2=MNCN,
而NO2=(x22+y2/span>2),MN=![]() (x2﹣x1),CN=
(x2﹣x1),CN=![]() x2,
x2,
即(x22+y22)=2x2(x2﹣x1),
即2x1x2=x22﹣y22,而y2=x2﹣3,
∴2x1x2=6x2﹣9
即2m=![]() ×6﹣9
×6﹣9
解得:m=![]() 或
或![]() (不符合题意,舍去).
(不符合题意,舍去).
∴m=![]()