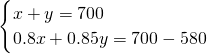题目内容
将直径为16cm的圆形铁皮,做成四个相同圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的高为________.
2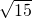 cm
cm
分析:算出圆形的周长,那么除以4就可求出一个圆锥侧面的弧长,那么除以2π求得圆锥的底面半径,利用勾股定理即可求得每个圆锥容器的高.
解答:直径为16cm,则半径为8,圆的周长=16π,
则每个扇形的弧长= =4πcm,
=4πcm,
所以做成的圆锥的底面半径r= =2cm,
=2cm,
由勾股定理得,圆锥容器的高=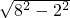 =2
=2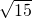 cm.
cm.
故答案为:2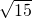 cm.
cm.
点评:本题考查了圆锥的运算,利用了勾股定理,圆的周长公式求解,牢记有关的公式是解决此题的关键.
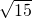 cm
cm分析:算出圆形的周长,那么除以4就可求出一个圆锥侧面的弧长,那么除以2π求得圆锥的底面半径,利用勾股定理即可求得每个圆锥容器的高.
解答:直径为16cm,则半径为8,圆的周长=16π,
则每个扇形的弧长=
 =4πcm,
=4πcm,所以做成的圆锥的底面半径r=
 =2cm,
=2cm,由勾股定理得,圆锥容器的高=
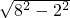 =2
=2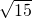 cm.
cm.故答案为:2
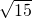 cm.
cm.点评:本题考查了圆锥的运算,利用了勾股定理,圆的周长公式求解,牢记有关的公式是解决此题的关键.

练习册系列答案
相关题目
张老师为了解班级学生双休日做数学作业所需时间的情况,随机抽查了本班级10名学生,结果如下表所示:
| 作业所需时间(分钟) | 90 | 100 | 120 | 150 | 200 |
| 人数 | 2 | 2 | 2 | 3 | 1 |
- A.150分钟
- B.135分钟
- C.120钟
- D.100分钟
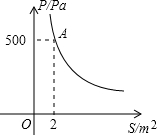 其图象如下图所示.
其图象如下图所示.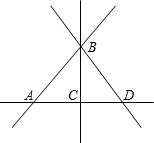 如图,A、C、D三点在一条直线上,观察图形,下列说法正确的个数是
如图,A、C、D三点在一条直线上,观察图形,下列说法正确的个数是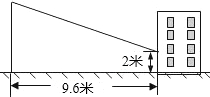 某同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影厂为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为米.
某同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影厂为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为米.