题目内容
 (2012•衢州二模)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE=
(2012•衢州二模)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE=| 1 | 4 |
(1)求证:CE=CF;
(2)若G在AD上,连接GC,且∠GCE=45°,求∠GCF的度数;
(3)在(2)的条件下,求GC的长度.
分析:(1)根据正方形性质得出BC=CD,∠BCD=∠B=∠ADC=∠CDF=90°,根据SAS证△EBC≌△FDC即可;
(2)求出∠BCE=∠DCF,求出∠BCE+∠DCG=45°,代入求出即可;
(3)连接EG,根据SAS证△ECG≌△FCG,推出EG=GF,设AG=x,求出EG=GF=5-x,在△AEG中根据勾股定理得出方程,求出AG,求出DG,根据勾股定理求出即可.
(2)求出∠BCE=∠DCF,求出∠BCE+∠DCG=45°,代入求出即可;
(3)连接EG,根据SAS证△ECG≌△FCG,推出EG=GF,设AG=x,求出EG=GF=5-x,在△AEG中根据勾股定理得出方程,求出AG,求出DG,根据勾股定理求出即可.
解答:(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠B=∠ADC=∠CDF=90°,
在△EBC和△FDC中
∵
,
∴△EBC≌△FDC(SAS),
∴CE=CF.
(2)解:∵△EBC≌△FDC,
∴∠BCE=∠DCF,
∵∠BCD=90°,∠GCE=45°,
∴∠BCE+∠GCD=90°-45°=45°,
∴∠GCD+∠DCF=45°,
∴∠GCF=45°.
(3)解:连接EG,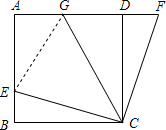
∠ECG=∠GCF=45°,
在△ECG和△FCG中
∵
,
∴△ECG≌△FCG,
∴EG=GF,
∵DF=BE=
BC=1,
∴BC=CD=AD=AB=4,
设AG=x,则DG=4-x,GF=4-x+1=5-x=EG,AE=4-1=3,
在Rt△AEG中,由勾股定理得:32+x2=(5-x)2,
解得:x=1.6,
DG=4-1.6=2.4,
在Rt△GCD中,由勾股定理得:GC=
=
.
∴BC=CD,∠BCD=∠B=∠ADC=∠CDF=90°,
在△EBC和△FDC中
∵
|
∴△EBC≌△FDC(SAS),
∴CE=CF.
(2)解:∵△EBC≌△FDC,
∴∠BCE=∠DCF,
∵∠BCD=90°,∠GCE=45°,
∴∠BCE+∠GCD=90°-45°=45°,
∴∠GCD+∠DCF=45°,
∴∠GCF=45°.
(3)解:连接EG,

∠ECG=∠GCF=45°,
在△ECG和△FCG中
∵
|
∴△ECG≌△FCG,
∴EG=GF,
∵DF=BE=
| 1 |
| 4 |
∴BC=CD=AD=AB=4,
设AG=x,则DG=4-x,GF=4-x+1=5-x=EG,AE=4-1=3,
在Rt△AEG中,由勾股定理得:32+x2=(5-x)2,
解得:x=1.6,
DG=4-1.6=2.4,
在Rt△GCD中,由勾股定理得:GC=
| 42+2.42 |
4
| ||
| 5 |
点评:本题考查了全等三角形的性质和判定,正方形的性质,勾股定理等知识点,用了方程思想,主要考查学生综合运用性质进行推理和计算的能力,题目比较好,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
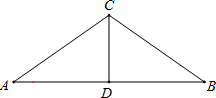 (2012•衢州二模)如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米,两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D.
(2012•衢州二模)如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米,两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D.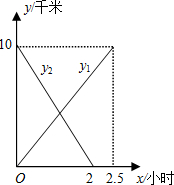 、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题:
、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题: