题目内容
【题目】已知:E、F是ABCD的对角线AC上的两点,AF=CE,求证:∠CDF=∠ABE. 
【答案】证明:∵AF=CE. ∴AE=CF,
∵在ABCD中,AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中, 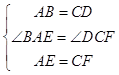 ,
,
∴△ABE≌△CDF(SAS),
∴∠CDF=∠ABE.
【解析】根据平行四边形的对边相等可得AB=CD,对边平行可得AB∥CD,再根据两直线平行,内错角相等可得∠BAE=∠DCF,然后利用“边角边”证明△ABE和△CDF全等,根据全等三角形对应边相等可得结论.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).

【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库。已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨。从甲、乙两库到A、B两库的路程和运费如下表(表中“元/吨·千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨·千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
【题目】某学校准备购买A、B两种型号篮球,询问了甲、乙两间学校了解这两款篮球的价格,下表是甲、乙两间学校购买A、B两种型号篮球的情况:
购买学校 | 购买型号及数量(个) | 购买支出款项(元) | |
A | B | ||
甲 | 3 | 8 | 622 |
乙 | 5 | 4 | 402 |
(1)求A、B两种型号的篮球的销售单价;
(2)若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个,求A种型号的篮球最少能采购多少个?




