题目内容
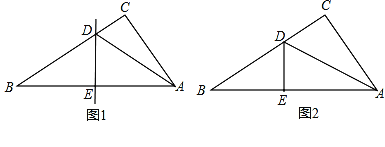
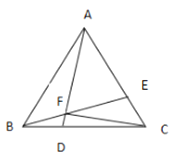
【题目】如图,已知![]() 中,
中,![]() ,
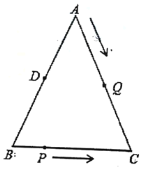
,![]() ,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
(2)若点P、Q两点分别从B、A两点同时出发,![]() 的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形?
的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形?
【答案】(1)△BPD与△CQP是全等.理由见解析;(2)经过1秒或2秒或1.8秒时,△CPQ是等腰三角形.
【解析】
(1)经过2秒后,PB=4m,PC=6m,AQ=8m,CQ=4m由已知可得BD=PC=6,BP=CQ=4,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP;
(2)可设点Q的运动时间为ts时△CPQ是等腰三角形,则可知PB=2tcm,PC=(10-2t)cm,AQ=4tcm,CQ=(12-4t)cm,再根据![]() 的周长为16cm,得出
的周长为16cm,得出![]() ,据(1)同理可得当CP=CQ时,当PQ=PC时,当QP=QC时,△CPQ为等腰三角形,列出方程,从而求得t的值.
,据(1)同理可得当CP=CQ时,当PQ=PC时,当QP=QC时,△CPQ为等腰三角形,列出方程,从而求得t的值.
(1)△BPD与△CQP是全等.理由如下:
当P,Q两点分别从B,A两点同时出发运动2秒时有BP=2×2=4cm,AQ=4×2=8cm,
则CP=BC-BP=10-4=6cm,CQ=AC-AQ=12-8=4cm ,
∵D是AB的中点,
∴BD=![]() AB=
AB=![]() ×12=6cm,
×12=6cm,
∴BP=CQ,BD=CP;
又∵△ABC中,AB=AC,
∴∠B=∠C ;
在△BPD和△CQP中
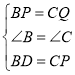
∴△BPD≌△CQP(SAS)
(2)设当P,Q两点同时出发运动t秒时,有BP=2t,AQ=4t,
∴t的取值范围为0<t≤3
则CP=10-2t,CQ=12-4t ,
∵△CPQ的周长为16cm,
∴PQ=16-(10-2t)-(12-4t)=6t-6
要使△CPQ是等腰三角形,则可分为三种情况讨论:
①当CP=CQ时,则有10-2t=12-4t,解得:t=1
②当PQ=PC时,则有6t-6=10-2t,解得:t=2;
③当QP=QC时,则有6t-6=12-4t,解得:t=1.8,
三种情况均符合t的取值范围.
综上所述,经过1秒或2秒或1.8秒时,△CPQ是等腰三角形.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】我县木瓜村盛产优种红富士苹果,曾推选参加省农产品博览会,某人去该地水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质都一样,市场售价都为6元/千克,但批发进价不相同.两家苹果批发进价如下:
A家规定:批发数量不超过1000千克,可按市场售价的92%优惠;批发数量多于1000千克但不超过2000千克,可全部按市场售价的90%优惠;批发数超过2000千克则全部按市场售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上部分 |
批发进价(元) | 市场售价的95% | 市场售价的85% | 市场售价的75% | 市场售价的70% |
[表格说明: ![]() 家苹果批发进价按分段计算,如:某人要批发苹果2100千克,则批发进价
家苹果批发进价按分段计算,如:某人要批发苹果2100千克,则批发进价![]() ]
]
根据上述信息,请解答下列问题:
(1)如果此人要批发1000千克苹果,则他在![]() 家批发需要_______元,在
家批发需要_______元,在![]() 家批发需要_______元;
家批发需要_______元;
(2)如果此人批发![]() 千克苹果(1500<x<2000),则他在
千克苹果(1500<x<2000),则他在![]() 家批发需要_______元,在
家批发需要_______元,在![]() 家批发需要_______元(用含
家批发需要_______元(用含![]() 的代数式表示);
的代数式表示);
(3)现在此人要批发3000千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
【题目】家家乐超市购进一批面粉,标准质量为50千克,现抽取20袋面粉进行称重检测,为记录的方便用![]() ,表示超过标准的重量,用
,表示超过标准的重量,用![]() 表示不足标准的重量,结果如下表(单位:千克)
表示不足标准的重量,结果如下表(单位:千克)
与标准差(千克) | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 |
袋数 | 3 | 2 | 3 | 4 | 1 | 2 | 1 | 4 |
(1)求这20袋面粉超出或不足的质量为多少?
(2)这20袋面粉平均每袋多少千克?