题目内容
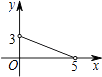
【题目】如图,在直角坐标系中,以点P为圆心的圆弧与x轴交于A,B两点,已知P(4,2)和A(2,0),则点B的坐标是 . 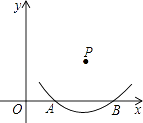
【答案】(6,0)
【解析】解:连接PA、PB.过点P作PD⊥AB于点D.
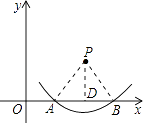
∵P(4,2)、A(2,0),
∴PA= ![]() =2
=2 ![]() ,PD=2;
,PD=2;
∵点P为圆心的圆弧与x轴交于A、B两点,
∴PA=PB=2 ![]() ,AB是垂直于直径的弦,
,AB是垂直于直径的弦,
∴AD=DB;
在直角三角形PDA中,AD2=AP2﹣PD2,
∴AD=2;
∴AB=4,
∴B(6,0).
所以答案是:B(6,0).
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.

练习册系列答案
相关题目