题目内容
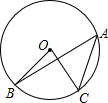 如图,已知圆心角∠BOC=78°,则圆周角∠BAC的度数是( )
如图,已知圆心角∠BOC=78°,则圆周角∠BAC的度数是( )| A、156° | B、78° | C、39° | D、12° |
分析:观察图形可知,已知的圆心角和圆周角所对的弧是一条弧,根据同弧所对的圆心角等于圆周角的2倍,由圆心角∠BOC的度数即可求出圆周角∠BAC的度数.
解答:解:∵圆心角∠BOC和圆周角∠BAC所对的弧为
,
∴∠BAC=
∠BOC=
×78°=39°.
故选C
 |
| BC |
∴∠BAC=
| 1 |
| 2 |
| 1 |
| 2 |
故选C
点评:此题要求学生掌握圆周角定理,考查学生分析问题、解决问题的能力,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知圆心角∠AOB的度数为100°,则圆周角∠ACB的度数是( )
如图,已知圆心角∠AOB的度数为100°,则圆周角∠ACB的度数是( )| A、80° | B、100° | C、120° | D、130° |
 如图,已知圆心角∠BOC=80°,那么圆周角∠BAC=
如图,已知圆心角∠BOC=80°,那么圆周角∠BAC=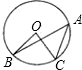 如图,已知圆心角∠BOC=80°,则圆周角∠BAC的度数是
如图,已知圆心角∠BOC=80°,则圆周角∠BAC的度数是 如图,已知圆心角∠BOC=110°,则∠BAC的度数是( )
如图,已知圆心角∠BOC=110°,则∠BAC的度数是( )