题目内容
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
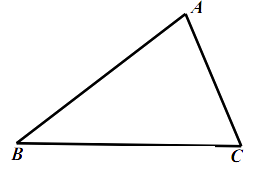
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD. 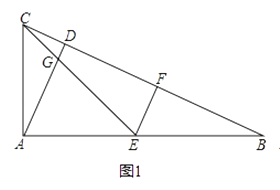
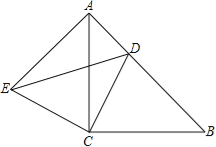
(2)如图2,AC:AB=1: ![]() ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值. 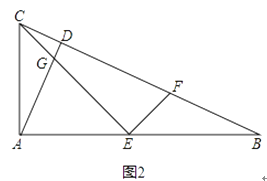
【答案】
(1)证明:如图1,

在△ABC中,∵∠CAB=90°,AD⊥BC于点D,
∴∠CAD=∠B=90°﹣∠ACB.
∵AC:AB=1:2,
∴AB=2AC,
∵点E为AB的中点,
∴AB=2BE,
∴AC=BE.
在△ACD与△BEF中,
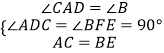 ,
,
∴△ACD≌△BEF,
∴CD=EF,即EF=CD
(2)解:如图2,作EH⊥AD于H,EQ⊥BC于Q,
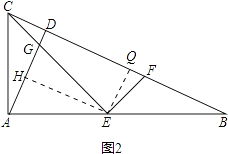
∵EH⊥AD,EQ⊥BC,AD⊥BC,
∴四边形EQDH是矩形,
∴∠QEH=90°,
∴∠FEQ=∠GEH=90°﹣∠QEG,
又∵∠EQF=∠EHG=90°,
∴△EFQ∽△EGH,
∴EF:EG=EQ:EH.
∵AC:AB=1: ![]() ,∠CAB=90°,
,∠CAB=90°,
∴∠B=30°.
在△BEQ中,∵∠BQE=90°,
∴sinB= ![]() =
= ![]() ,
,
∴EQ= ![]() BE.
BE.
在△AEH中,∵∠AHE=90°,∠AEH=∠B=30°,
∴cos∠AEH= ![]() =
= ![]() ,
,
∴EH= ![]() AE.
AE.
∵点E为AB的中点,
∴BE=AE,
∴EF:EG=EQ:EH= ![]() BE:
BE: ![]() AE=1:
AE=1: ![]() =
= ![]() :3
:3
【解析】(1)根据同角的余角相等得出∠CAD=∠B,根据AC:AB=1:2及点E为AB的中点,得出AC=BE,再利用AAS证明△ACD≌△BEF,即可得出EF=CD;(2)作EH⊥AD于H,EQ⊥BC于Q,先证明四边形EQDH是矩形,得出∠QEH=90°,则∠FEQ=∠GEH,再由两角对应相等的两三角形相似证明△EFQ∽△EGH,得出EF:EG=EQ:EH,然后在△BEQ中,根据正弦函数的定义得出EQ= ![]() BE,在△AEH中,根据余弦函数的定义得出EH=
BE,在△AEH中,根据余弦函数的定义得出EH= ![]() AE,又BE=AE,进而求出EF:EG的值.
AE,又BE=AE,进而求出EF:EG的值.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少.(如下表) 甲超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 5 | 10 | 5 |
乙超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 10 | 5 | 10 |
(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.