题目内容
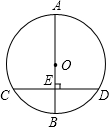已知：如图，⊙O中直径AB垂直于弦CD，垂足为E，若AB=10，CD=6，则BE的长是（ ）| A、1 | B、2 | C、3 | D、4 |
分析：先求出半径和CE的长度，再利用勾股定理求出弦心距OE的长，BE就等于半径与弦心距的差．
解答：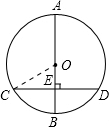
解：如图，连接OC，∵AB=10，
∴半径OC=10÷2=5，
∵CD=6，
∴CE=6÷2=3，
根据勾股定理OE=
=
=4，
∴BE=5-4=1．
故选A．
解：如图，连接OC，∵AB=10，∴半径OC=10÷2=5，
∵CD=6，
∴CE=6÷2=3，
根据勾股定理OE=
| OC2-CE2 |
| 52-32 |
∴BE=5-4=1．
故选A．
点评：本题主要是半径、弦心距、半弦所构成的直角三角形的勾股定理的运用，是考查垂径定理的常考题型．
练习册系列答案
名校课堂系列答案
相关题目
已知：如图，⊙O中直径AB垂直于弦CD，垂足为E，若AB=10，CD=6，则BE的长是
