��Ŀ����
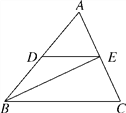
����Ŀ��С����Ҫ����ѧУʳ�ú�ʳ����ǰ��һ�����ĸ߶ȣ�����ʳ��¥��M����������ǰ��3����A�������������E������Ϊ30�㣬���ּ�������̨����C����������Ķ���E��������60�㣬�ټ�����ǰ�ߵ�������D�������ʳ��¥��N������Ϊ45�㣮��֪A�������ĸ߶�AB=2�ף���BCA=30�㣬��B��C��D������ͬһֱ���ϣ�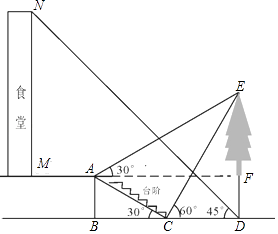
��1������DE�ĸ߶ȣ�
��2����ʳ��MN�ĸ߶ȣ�
���𰸡�
��1���⣺��ͼ����DE=x��
��AB=DF=2��
��EF=DE��DF=x��2��
�ߡ�EAF=30�㣬
��AF= ![]() =
= ![]() =
= ![]() ��x��2����
��x��2����
�֡�CD= ![]() =
= ![]() =
= ![]() x��BC=
x��BC= ![]() =
= ![]() =2
=2 ![]() ��
��
��BD=BC+CD=2 ![]() +
+ ![]() x
x
��AF=BD�ɵ� ![]() ��x��2��=2
��x��2��=2 ![]() +
+ ![]() x��
x��
��ã�x=6��
����DE�ĸ߶�Ϊ6�ף�
��2���⣺�ӳ�NM��DB�ӳ����ڵ�P����AM=BP=3��
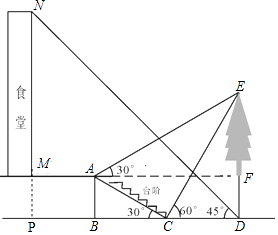
�ɣ�1��֪CD= ![]() x=
x= ![]() ��6=2
��6=2 ![]() ��BC=2
��BC=2 ![]() ��
��
��PD=BP+BC+CD=3+2 ![]() +2
+2 ![]() =3+4
=3+4 ![]() ��
��
�ߡ�NDP=45�㣬��MP=AB=2��
��NP=PD=3+4 ![]() ��
��
��NM=NP��MP=3+4 ![]() ��2=1+4
��2=1+4 ![]() ��
��
��ʳ��MN�ĸ߶�Ϊ1+4 ![]() �ף�
�ף�
����������1�������Ǻ������з��̣���Rt![]() AEF�пɸ��ݡ�EAF=30�㣬���������г�����tan��EAF=
AEF�пɸ��ݡ�EAF=30�㣬���������г�����tan��EAF=![]()
![]() ,���x;��2����45��Ƿŵ�Rt
,���x;��2����45��Ƿŵ�Rt![]() NPD�У�������ӳ�NM��������P��NP=PD=3+BC+CD=3+
NPD�У�������ӳ�NM��������P��NP=PD=3+BC+CD=3+![]() ,���ʳ��MN�ĸ߶�Ϊ��3+
,���ʳ��MN�ĸ߶�Ϊ��3+![]() -2�� ��=��1+
-2�� ��=��1+![]() ����.
����.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ���ܺ���Ӱ�죬�Ա����ϵĵ���ȡů�����ۻ�����ij��������ÿ̨�ɱ��۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ���ȡů�����±��ǽ���������������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȡů�������۵��ۣ�
��2�����������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȡů����30̨����A���ͺŵĵ���ȡů������ܲɹ�����̨��