题目内容
如图,△ABC中,∠CAB与∠CBA均为锐角,分别以CA、CB为边向△ABC外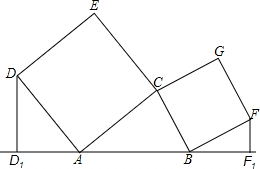 侧作正方形CADE和正方形CBFG,再作DD1⊥直线AB于D1,FF1⊥直线AB于F1.
侧作正方形CADE和正方形CBFG,再作DD1⊥直线AB于D1,FF1⊥直线AB于F1.求证:(Ⅰ)DD1+FF1=AB;
(Ⅱ)线段AB的中点N也平分线段D1F1.
分析:(1)过点C作CH⊥AB,垂足为H;再通过两对全等三角形来证明DD1+EE1=AB即可;
(3)利用“梯形的中位线长等于两底和的一半”,设M为DE的中点,Q为D1E1的中点,MQ=
AB且MQ⊥AB,特殊地,当四边形DD1E1E为矩形时,以上结论仍然成立.又因为可证明D1A=E1B,所以AB的中点N就是D1E1的中点.
(3)利用“梯形的中位线长等于两底和的一半”,设M为DE的中点,Q为D1E1的中点,MQ=
| 1 |
| 2 |
解答: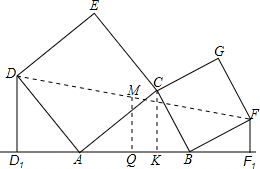 证明:(1)过点C作CK⊥AB于K,
证明:(1)过点C作CK⊥AB于K,
∵DD1⊥AB、EE1⊥AB,
∴∠DD1A=∠EE1B=∠AKC=∠BKC=90°,
∴∠DAD1+∠CAB=∠CAE+∠ACK=∠CBK+∠BCK=∠CBK+∠EBE1=90°,
∴∠DAD1=∠ACK,∠EBE1=∠BCK,
∵AD=AC,BC=BE,
∴△ADD1≌△CAK,△EBE1≌△BCK,
∴DD1=AK,EE1=BK,
∴DD1+EE1=AB;
(2)设M为DF的中点,Q为D1F1的中点,
则:MQ=
(DD1+EE1)=
AB且MQ⊥AB,
当四边形DD1E1E为矩形时,以上结论仍然成立.
∴△ADD1≌△CAK,△EBE1≌△BCK,
又∵D1A=CK=E1B,
∴AB的中点N就是D1E1的中点.
 证明:(1)过点C作CK⊥AB于K,
证明:(1)过点C作CK⊥AB于K,∵DD1⊥AB、EE1⊥AB,
∴∠DD1A=∠EE1B=∠AKC=∠BKC=90°,
∴∠DAD1+∠CAB=∠CAE+∠ACK=∠CBK+∠BCK=∠CBK+∠EBE1=90°,
∴∠DAD1=∠ACK,∠EBE1=∠BCK,
∵AD=AC,BC=BE,
∴△ADD1≌△CAK,△EBE1≌△BCK,
∴DD1=AK,EE1=BK,
∴DD1+EE1=AB;
(2)设M为DF的中点,Q为D1F1的中点,
则:MQ=
| 1 |
| 2 |
| 1 |
| 2 |
当四边形DD1E1E为矩形时,以上结论仍然成立.
∴△ADD1≌△CAK,△EBE1≌△BCK,
又∵D1A=CK=E1B,
∴AB的中点N就是D1E1的中点.
点评:此题考查了全等三角形的判定与性质,正方形的性质,以及梯形中位线的性质等知识.此题综合性很强,注意数形结合思想的应用.

练习册系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.