题目内容
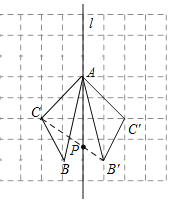
【题目】如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线l成轴对称的△AB′C′；
（2）在直线l上找一点P，使PB′+PC的长最短；
（3）若△ACM是以AC为腰的等腰三角形，点M在小正方形的顶点上．这样的点M共有 个．
【答案】（1）见解析；（2）见解析；（3）4.
【解析】
（1）依据轴对称的性质得到各顶点，进而得出与△ABC关于直线l成轴对称的△AB′C′；
（2）依据两点之间，线段最短，连接B'C交直线l于点P，则PB′+PC的长最短；
（3）分别以点A和点B为圆心，AB长为半径画弧，即可得到符合条件的点M．
解：（1）如图所示，△AB′C′即为所求；
（2）如图所示，点P即为所求；
（3）如图所示，符合条件的点M共有4个，
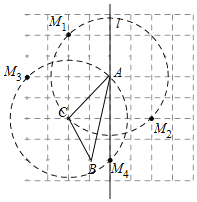
故答案为：4．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的价目表如下（注：水费按月份结算）：
价目表 | |
每月用水量 | 单价 |
不超过6 | 2元/ |
超出6 | 4元/ |
超出10 | 8元 |
请根据上表的内容解答下列问题：
（1）填空：若该户居民2月份用水5
，则应交水费 元；3月份用水8，则应收水费 元；
（2）若该户居民4月份用水
（其中
），则应交水费多少元（用含的代数式表示，并化简）；
（3）若该户居民5、6两个月共用水14（6月份用水量超过了5月份），设5月份用水
，直接写出该户居民5、6两个月共交水费多少元（用含的代数式表示）．
